DISEQUAZIONI FRATTE CON VALORE ASSOLUTO
- Disequazioni fratte
- Disequazioni con valore assoluto
- Disequazioni fratte con valore assoluto
- Disequazioni fratte con valore assoluto a numeratore o a denominatore
- Disequazioni fratte con valore assoluto a numeratore o a denominatore
Continuiamo l'esame delle DISEQUAZIONI FRATTE con VALORE ASSOLUTO iniziato nella lezione precedente ed occupiamoci delle disequazioni che si presentano nella forma
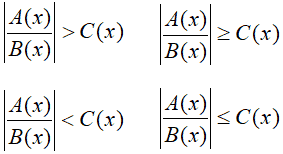
Queste disequazioni si risolvono in maniera analoga a disequazioni del tipo:
|D(x)| > C(x) |D(x)| ≥ C(x)
|D(x)| < C(x) |D(x)| ≤ C(x).
Occorrerà ricordarsi sempre di porre il DENOMINATORE DIVERSO DA ZERO per le ragioni che abbiamo illustrato nella lezione precedente.
Vediamo un esempio per comprendere meglio come procedere.
Esempio:
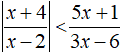
Nelle disequazioni del tipo
|D(x)| ≥ C(x)
avevamo detto che, per prima cosa dobbiamo studiare il segno della espressione presente nel modulo.
Quindi si tratta di risolvere:
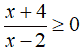
Dallo studio delle disequazioni sappiamo che occorre studiare separatamente il segno del numeratore e quello del denominatore. Quindi:
- NUMERATORE
x + 4 ≥ 0
x ≥ - 4
-
DENOMINATORE
x - 2 > 0
Al denominatore mettiamo solamente il segno di maggiore, e non quello di uguale, dato che dobbiamo escludere il caso in cui il denominatore sia uguale a zero per le osservazioni fatte sopra.
Avremo
x > 2.
Andiamo a studiare il segno della nostra frazione:
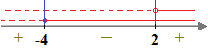
La frazione è positiva, o uguale a zero, quando
x < -4 ˅ x > 0
che si legge
x minore o uguale di meno -4
oppure
x maggiore di 2.
A questo punto dobbiamo vedere come cambia la nostra disequazione con valore assoluto, al variare del valore della frazione presente nel modulo. Disegniamo il risultato ottenuto su un altro grafico:
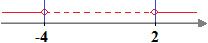
Il grafico è diviso in tre parti, quindi dobbiamo scrivere e risolvere tre sistemi:
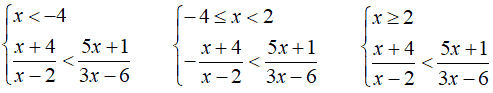
Iniziamo col risolvere il primo sistema.
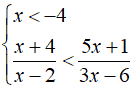
Occupiamoci della seconda delle due disequazioni. Calcoliamo il minimo comune denominatore e moltiplichiamo entrambe per esso. Otterremo
(3x - 6) · (x + 4) < (5x + 1) · (x - 2)
3x2 + 12x -6x -24 < 5x2 - 10x + x - 2
3x2 - 5x2 + 12x - 6x + 10x - x - 24 + 2 < 0
-2x2 + 15x - 22 < 0
2x2 - 15x + 22 > 0
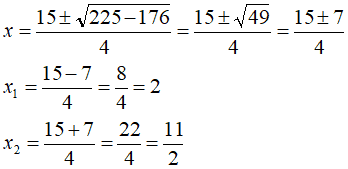
Le soluzioni della disequazione sono
x < 2 ˅ x > 11/2.
Le soluzioni del sistema sono
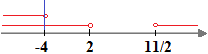
ovvero
x < - 4.
Passiamo al secondo sistema.
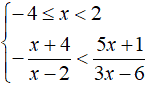
Occupiamoci della seconda delle due disequazioni. Avremo:
(3x - 6) · (-x - 4) < (5x + 1) · (x - 2)
- 3x2 - 12x + 6x + 24 < 5x2 - 10x + x - 2
- 3x2 - 5x2 - 12x + 6x + 10x - x + 24 + 2 < 0
-8x2 + 3x + 26 < 0
8x2 - 3x - 26 > 0
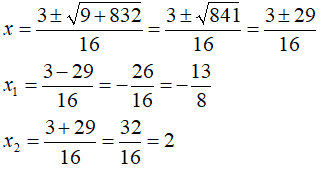
Le soluzioni della disequazione sono
x < -13/8 ˅ x > 2.
Le soluzioni del sistema sono
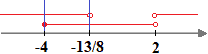
ovvero
- 4 ≤ x < - 13/8.
Concludiamo con l'ultimo sistema:
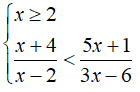
La seconda disequazione l'abbiamo già risolta e sappiamo che le sue soluzioni sono:
x < 2 ˅ x > 11/2.
Il sistema, quindi, avrà le seguenti soluzioni:

x > 11/2.
Le soluzioni della disequazione di partenza, quindi, sono:
x < - 4 ˅ - 4 < x < -13/8 ˅ x > 11/2
ma poiché
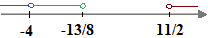
possiamo scrivere la nostra soluzione come
x < -13/8 ˅ x > 11/2.
Nella prossima lezione continueremo ancora a parlare delle disequazioni fratte con valore assoluto.






