AREA DI UN POLIGONO IRREGOLARE
- Poligoni equivalenti
- Figure equicomposte ed equiscomponibili
- Area dei poligoni
- Area del triangolo rettangolo
- Area del rettangolo
- Area del trapezio
- Poligoni equiangoli poligoni equilateri poligoni regolari
- I poligoni
- Misure di superficie
In alcuni casi può capitare di dover trovare l'AREA di un POLIGONO IRREGOLARE.
In questi casi non è possibile applicare le formule che abbiamo visto nelle lezioni precedenti.
Per poter calcolare l'AREA di un POLIGONO IRREGOLARE, il metodo più semplice è il seguente:
- cerchiamo di SCOMPORRE il poligono irregolare in POLIGONI REGOLARI;
- calcoliamo l'AREA dei POLIGONI REGOLARI nei quali abbiamo scomposto il poligono irregolare;
- SOMMIAMO le AREE dei POLIGONI REGOLARI trovati in modo da ottenere l'area del poligono irregolare.
Esempio:
dato il poligono ABCDEF
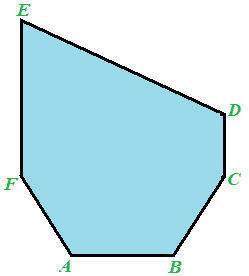
calcolarne l'area.
Osservando bene l'immagine notiamo che il nostro poligono può essere scomposto in tre poligoni regolari: che abbiamo indicato rispettivamente con i numeri 1, 2 e 3:
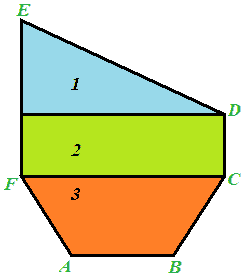
Il primo poligono è un triangolo rettangolo, il secondo un rettangolo, il terzo un trapezio.
Ora supponiamo di sapere che:
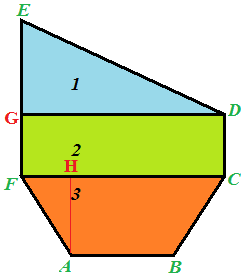
- il segmento AB misura 10,5 cm;
- il segmento FC misura 40 cm;
- il segmento AH misura 14 cm;
- il segmento FG misura 12 cm;
- il segmento GE misura 19 cm.
Iniziamo con il calcolare l'area del triangolo rettangolo:
AT = (c1 x c2)/2
dove
AT = area del triangolo rettangolo
c1 (che si legge c con uno) = un cateto
c2 (che si legge c con due) = l'altro cateto.
Ora noi sappiamo che il cateto GE misura 19 cm. Il cateto GD è congruo al segmento FC, quindi misura 40 cm. Quindi avremo:
AT
= (c1 x
c2)/2 = (19 x 40)/ 2 =760/ 2 = 380 cm2.
Passiamo quindi a calcolare l'area del rettangolo:
AR = b x h
dove
AR = area del rettangolo
b = base
h = altezza.
La base del rettangolo è il segmento FC che misura 40 cm, mentre l'altezza è il segmento FG che misura 12 cm. Quindi avremo:
AR
= b x h = 40 x 12 = 480 cm2.
Infine calcoliamo l'area del trapezio:
ATR = [(b1 + b2) x h]/2
dove
ATR = area del trapezio
b1 = base maggiore
b2 = base minore
h = altezza.
La base maggiore è il segmento FC che misura 40 cm. La base minore è il segmento AB che misura 10,5 cm. L'altezza è il segmento AH che misura 14 cm. Quindi:
ATR = [(b1 + b2) x h]/2 = [(40+10,5) x 14]/2 =
=
[50,5 x 14]/ 2 = 707/ 2 = 353,50 cm2.
A questo punto possiamo calcolare l'area del nostro poligono dato dalla somma delle tre aree appena trovate:
A = AT + AR + ATR =
= 380 + 480 + 353,50 =1.213,50 cm2.






