AREA DEL TRIANGOLO RETTANGOLO
- Area dei poligoni
- Area del triangolo
- Area del triangolo e formule inverse
- Triangoli
- Triangolo rettangolo
- Misure di superficie
In una delle precedenti lezioni abbiamo visto che l'AREA DEL TRIANGOLO si ottiene MOLTIPLICANDO la misura della BASE per la relativa ALTEZZA e DIVIDENDO il prodotto ottenuto per 2.
Quindi, la formula da applicare per calcolare l'AREA DEL TRIANGOLO è la seguente:
A = (b x h)/2
dove
A = area del triangolo
b = base
h = altezza.
Sempre in quella lezione abbiamo affermato che quanto detto vale per OGNI TIPO DI TRIANGOLO.
Ora, esaminiamo per un istante il caso del TRIANGOLO RETTANGOLO:
Nel triangolo rettangolo un CATETO è la BASE del triangolo, mentre l'altro CATETO è l'altezza ad essa relativa. Ovvero:
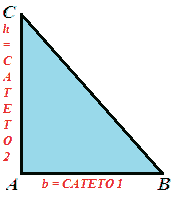
Quindi l'AREA DEL TRIANGOLO RETTANGOLO si ottiene MOLTIPLICANDO le misure dei DUE CATETI e DIVIDENDO il prodotto ottenuto per 2.
Ovvero:
A = (c1 x c2)/2
dove
A = area del triangolo rettangolo
c1 (che si legge c con uno) = un cateto
c2 (che si legge c con due) = l'altro cateto.
Esempio:
calcolare l'area di un triangolo rettangolo i cui cateti misurano rispettivamente cm 7 e cm 8.
A = (c1 x c2)/2 = (7 x 8)/2 = 56/2 = cm2 28.
L'area del triangolo rettangolo misura 28 cm2.






