AREA DI UNA FASCIA POLIGONALE
Si chiama FASCIA POLIGONALE la PARTE di PIANO delimitata da DUE POLIGONI, di cui uno è interno all'altro, aventi i LATI PARALLELI ed EQUIDISTANTI.
Quella che vedete disegnata sotto è un esempio di FASCIA POLIGONALE:

L'AREA di una FASCIA POLIGONALE è data dalla DIFFERENZA tra l'AREA del POLIGONO ESTERNO e l'AREA del POLIGONO INTERNO.
Esempio:
due quadrati con i lati rispettivamente di cm 10 e cm 15 hanno i lati paralleli ed equidistanti. Calcolare l'area della figura colorata:
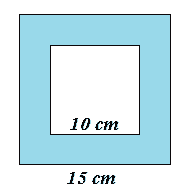
Cominciamo con il calcolare l'area del quadrato esterno, il cui lato misura cm 15:
A = l2
dove
A = area del quadrato
l = lato del quadrato.
A = l2 = 152 = 225 cm2.
Ora calcoliamo l'area del quadrato interno, il cui lato misura cm 10:
A = l2 = 102 = 100 cm2.
L'area della fascia poligonale è data dalla differenza tra l'area del quadrato esterno e l'area di quello interno:
225 - 100 = 125 cm2.






