PRODOTTO DI DUE TRASLAZIONI
Supponiamo di avere una FIGURA PIANA che chiameremo F: nel nostro caso sarà un triangolo.
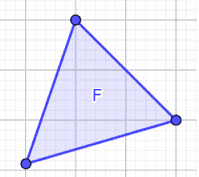
Nelle lezioni precedenti abbiamo avuto modo di vedere come
si effettua la TRASLAZIONE T di vettore
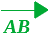in modo da ottenere, dalla figura F, la figura
F'.
Quindi, dato il vettore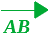
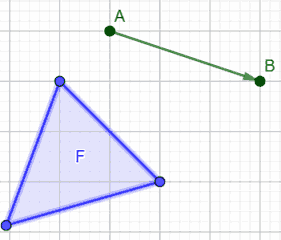
costruiamo la traslazione di T di vettore
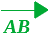ed otteniamo la la figura
F'.
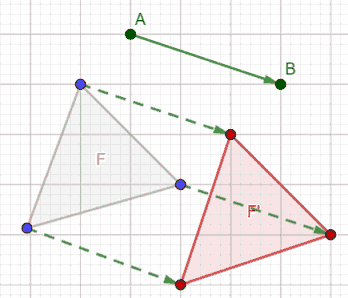
In questo modo, data la figura piana F, abbiamo costruito la sua trasformata
F' rispetto ad una trasformazione T di vettore
.
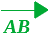Ora, data la figura F', vogliamo ottenere la figura
F'' mediante un'altra traslazione, questa volta, di vettore
.
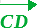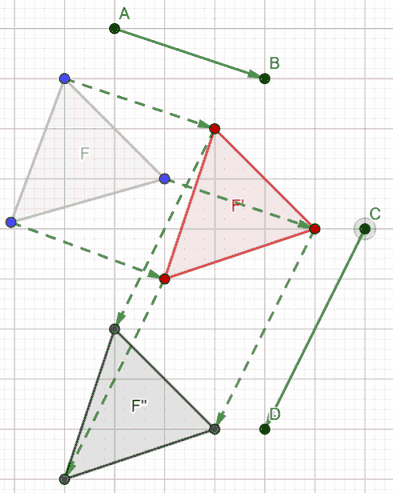
La figura F è stata trasformata nelle figura F'' mediante il PRODOTTO di due TRASLAZIONI.
E' abbastanza evidente che, partendo dalla figura F, avremmo potuto ottenere
direttamente la figura
F'' mediante la traslazione di vettore
.
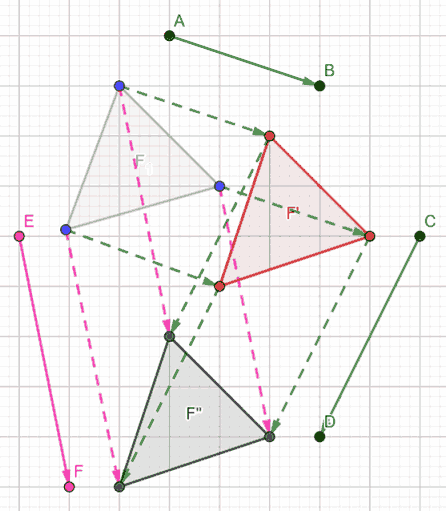
Quindi possiamo affermare che il PRODOTTO di due TRASLAZIONI è ancora una traslazione.
