FIGURE OTTENUTE PER TRASLAZIONE
- Vettore
- Il punto
- La retta
- Il segmento
- Figure geometriche congruenti e figure geometriche equivalenti
Dopo aver introdotto, nella precedente lezione il concetto di TRASLAZIONE, in questa lezione ci occuperemo della TRASLAZIONE di una FIGURA PIANA.
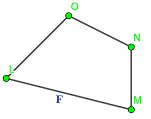
Disegniamo, una figura piana che chiameremo F.
Quindi disegniamo il vettore 
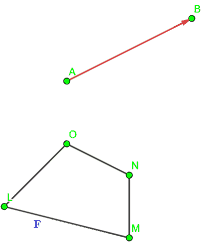
Fissiamo un punto P
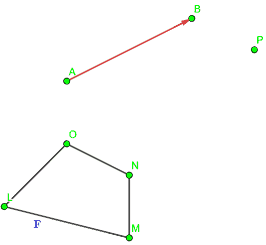
e conduciamo dal punto P la PARALLELA ad AB.
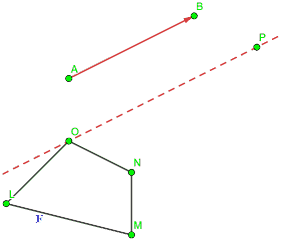
Ora stacchiamo, sulla retta che abbiamo appena disegnato, un segmento la cui lunghezza sia uguale al MODULO del vettore AB.
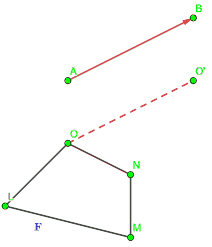
Ripetiamo questa costruzione per ogni punto della figura F.
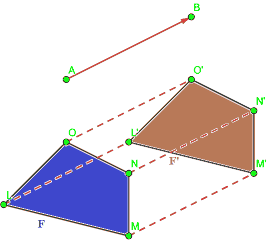
Quella che abbiamo ottenuto è la figura F'.
Si è dato, così, origine ad una CORRISPONDENZA BIUNIVOCA tra le due figure F ed F', dato che ad ogni punto di F corriponde un solo punto di F' e viceversa.
Questa corrispondenza prende il nome di TRASLAZIONE e si indica con la lettera T maiuscola.
I punti O ed O',
N ed N',
M ed M', e così via
si dicono OMOLOGHI o CORRISPONDENTI nella traslazione T
di vettore
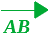
.
La DIREZIONE ed il VERSO del vettore AB sono anche la direzione ed il verso della TRASLAZIONE. Il modulo del vettore rappresenta l'AMPIEZZA della TRASLAZIONE.
Per effettuare la traslazione T è sufficiente TRASLARE i VERTICI
della figura F secondo il vettore 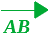 .
.
Ora ricalchiamo su un foglio di carta trasparente la figura F
e sovrapponiamola alla figura F': noteremo che le due figure coincidono in ogni loro punto.
Quindi possiamo dire che due figure piane F ed F' ottenute per
TRASLAZIONE sono
CONGRUENTI.
Nella prossima lezione parleremo di traslazioni orizzontali, verticali ed oblique.






