LA ROTAZIONE
Disegniamo, su un piano α (che si legge alfa), un PUNTO O:
Disegniamo, ora un ANGOLO β (che si legge beta).
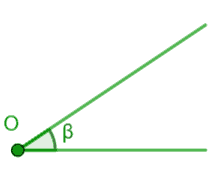
Ora associamo al nostro angolo un VERSO, che potrà essere orario oppure antiorario: in questo modo avremo un ANGOLO ORIENTATO che avrà una sua precia AMPIEZZA detta MODULO.
Nel nostro caso vogliamo associare al l'angolo β il verso orario:
Un ANGOLO ORIENTATO si indica con una FRECCIA sopra la lettera che lo individua: la freccia andrà da sinistra verso destra per indicare il verso orario e da destra verso sinistra per indicare il verso antiorario.
Angolo orientato con verso ORARIO:
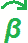
Angolo orientato con verso ANTIORARIO:
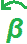
Nel nostro caso abbiamo disegnato un angolo con verso orario.
Ora, dato un qualsiasi punto P, del piano α,
il punto fisso O e un angolo orientato, 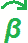, disegniamo
il corrispondente punto P' nel modo che segue:
- puntiamo il compasso in O;
- apriamo il compasso in modo che l'apertura sia uguale al segmento OP;
- descriviamo un arco corrispondente all'ampiezza dell'angolo in senso orario.
L'estremità P' dell'arco è il CORRISPONDENTE di P .
Più esattamente il punto P' si dice CORRISPONDENTE o OMOLOGO di P nella ROTAZIONE R.
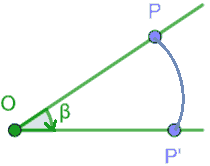
Il movimento diretto che ci ha permesso di passare dal punto P al punto P' prende il nome di ROTAZIONE: nel nostro esempio abbiamo eseguito una ROTAZIONE ORARIA di AMPIEZZA β.
Possiamo allora dire che la ROTAZIONE è un movimento diretto determinato, da:
- un punto fisso O, detto CENTRO DI ROTAZIONE,
- da un ANGOLO ORIENTATO che ne determina l'ampiezza,
- da un VERSO di spostamento.
Nella prossima lezione vedremo come si può effettuare la rotazione di una figura piana.
