ANGOLI ADIACENTI DEL PARALLELOGRAMMA
- Parallelogramma
- Angolo consecutivi e angoli adiacenti
- Angoli formati da due rette parallele tagliate da una trasversale
- Angoli complementari, angoli supplementari, angoli esplementari
In questa lezione ci soffermeremo ad esaminare gli ANGOLI ADIACENTI ad uno stesso lato del PARALLELOGRAMMA.
Ricordiamo che due ANGOLI si dicono ADIACENTI quando APPARTENGONO AD UNA STESSA RETTA.
Di seguito abbiamo disegnato un parallelogramma.
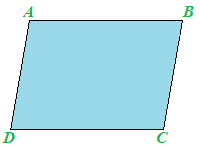
Gli angoli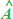 
e 
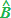sono adiacenti al
lato AB.
Gli angoli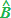
e 
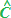sono adiacenti al
lato BC.
Gli angoli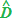 
e
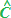sono adiacenti al
lato DC.
Gli angoli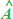
e
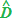sono adiacenti al
lato AD.
Dallo studio delle rette parallele sappiamo che, se disegniamo due rette parallele (a e b) e una retta r che interseca le prime due, si formano otto angoli che abbiamo indicato, nella figura sotto, ognuno con un colore diverso.
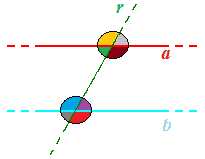
Ora osserviamo i due angoli che sotto abbiamo indicato con il colore grigio:
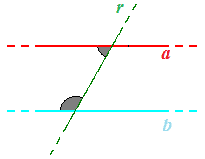
I due angoli si dicono ANGOLI CONIUGATI INTERNI: tali angoli sono SUPPLEMENTARI, cioè la loro somma è pari a 180°.
Mettiamo a confronto le due figure sopra:
I lati AB e DC del parallelogramma, per definizione, sono tra loro paralleli.
Il lato BC del parallelogramma interseca i due lati AB e DC.
Di
conseguenza, possiamo affermare che, gli angoli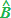
e
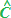sono ANGOLI CONIUGATI INTERNI e
quindi SUPPLEMENTARI.
Un
discorso analogo possiamo fare per gli angoli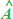
e .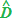
Osservando il nostro parallelogramma possiamo dire che anche i lati AD e BC sono paralleli tra loro.
Il lato AB del parallelogramma interseca i due lati AD e BC.
Di conseguenza, possiamo affermare che, gli
angoli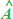
e
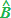sono ANGOLI CONIUGATI INTERNI e
quindi SUPPLEMENTARI.
Un
discorso analogo possiamo fare per gli angoli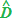
e .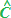
Quindi possiamo concludere che in un PARALLELOGRAMMA gli ANGOLI ADIACENTI allo stesso lato sono SUPPLEMENTARI.
