ANGOLI INTERNI ED ANGOLI ESTERNI DI UN POLIGONO
- I poligoni
- Caratteristiche dei poligoni
- Angolo consecutivi e angoli adiacenti
- Angoli complementari, angoli supplementari, angoli esplementari
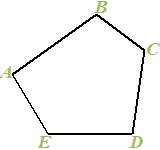
Disegniamo il nostro POLIGONO ABCDE:
Ora soffermiamoci ad osservare l'angolo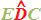 
:
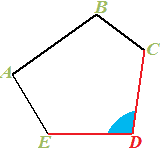
Il nostro angolo è formato da DUE LATI CONSECUTIVI, cioè DUE LATI aventi un VERTICE COMUNE.
Infatti, i lati ED e DC hanno il vertice D in comune.
Un angolo di questo tipo si chiama ANGOLO INTERNO del POLIGONO.
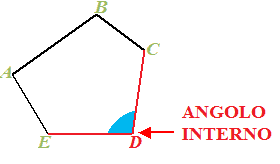
Generalizzando, quindi, possiamo dire che gli ANGOLI INTERNI del poligono sono quegli angoli FORMATI DA DUE LATI COSECUTIVI.
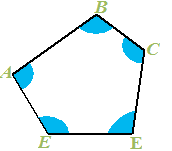
Nell'immagine sottostante, abbiamo evidenziato in AZZURRO gli ANGOLI INTERNI del poligono:
Ora osserviamo l'angolo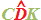 
:
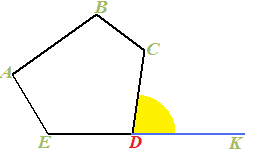
Questo angolo è formato da:
- un lato del poligono (il lato CD);
- il prolungamento di uno dei lati consecutivi (il prolungamento del lato ED).
L'angolo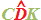
è un ANGOLO ESTERNO.
Quindi, si dicono ANGOLI ESTERNI del poligono, gli angoli formati da UN LATO del poligono e dal PROLUNGAMENTO di uno dei LATI CONSECUTIVI.
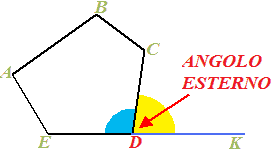
Ora osserviamo questa immagine:
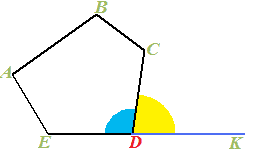
Nel disegno precedente abbiamo
evidenziato l'angolo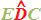
e l'angolo .
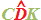Questi due angoli hanno il VERTICE COMUNE (D).
Notiamo che i due ANGOLI sono ADIACENTI. Ricordiamo che due angoli si dicono ADIACENTI se sono CONSECUTIVI e hanno i due lati non comuni (ED e DK) che APPARTENGONO AD UNA STESSA RETTA.
Sappiamo, inoltre, che due ANGOLI ADIACENTE sono SUPPLEMENTARI, cioè la loro somma misura 180°, come si vede chiaramente dal disegno precedente.
Quindi possiamo dire che, OGNI ANGOLO ESTERNO è ADIACENTE, e quindi SUPPLEMENTARE, dell'ANGOLO INTERNO avente lo STESSO VERTICE.
