TEOREMA DI ROUCHE' CAPELLI
- Matrice
- Rango o caratteristica di una matrice
- Sistemi di equazioni lineari algebriche
- Sistemi di equazioni e matrici
- Risoluzione di sistemi di equazioni lineari
- Equazioni ridotte a forma normale
Il TEOREMA di ROUCHE'-CAPELLI permette di stabilire se un SISTEMA e' POSSIBILE prima di averlo risolto.
Esso afferma che CONDIZIONE NECESSARIA e SUFFICIENTE affinché un sistema di equazioni lineari algebriche sia POSSIBILE è che la MATRICE DEI COEFFICIENTI e la MATRICE COMPLETA abbiano lo STESSO RANGO.
Esempio.
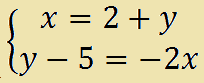
Riduciamo le due EQUAZIONI a FORMA NORMALE e mettiamo le incognite nello stesso ordine in modo da incolonnarle. Avremo:
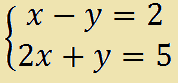
Ora scriviamo la MATRICE DEI COEFFICIENTI:
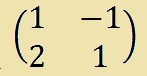
Il determinante della matrice data è
(1 · 1) - (-1 · 2) = 1 - (-2) = 3.
Essendo esso diverso da zero possiamo dire che la matrice ha rango 2.
Ora scriviamo la MATRICE COMPLETA:
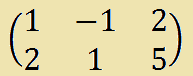
Trattandosi di una matrice non quadrata di ordine 3x2, e poiché sappiamo già che esiste una sottomatrice di ordine 2 con determinante non nullo, possiamo dire che il rango della matrice completa non potrà che essere 2.
Poiché il
RANGO DELLA MATRICE DEI COEFFICIENTI
=
RANGO DELLA MATRICE COMPLETA
il nostro SISTEMA è POSSIBILE.






