SOLUZIONI DI SISTEMI DI EQUAZIONI LINEARI
Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:
- Matrice
- Matrice identità
- Sistemi di equazioni lineari algebriche
- Sistemi di equazioni equivalenti
- Sistemi di equazioni e matrici
- Equazioni ridotte a forma normale
Iniziamo a vedere un primo metodo di SOLUZIONE dei SISTEMI DI EQUAZIONI LINEARI ALGEBRICHE per mezzo delle matrici.
Questo metodo si basa sul concetto di SISTEMI EQUIVALENTI.
Dato un sistema di equazioni lineari algebriche si procede nel modo seguente:
- si scrivono tutte le EQUAZIONI in FORMA NORMALE e si mettono le incognite tutte nello stesso ordine;
- si scrive la MATRICE COMPLETA del sistema. Per rendere più chiari i risultati che si otterranno successivamente scriviamo la matrice dei coefficienti e separiamo con una linea la colonna dei termini noti;
- si eseguono sulla matrice scritta
una serie di TRASFORMAZIONI in
modo da trasformare la MATRICE DEI SOLI
COEFFICIENTI in una MATRICE
IDENTITA' del tipo:
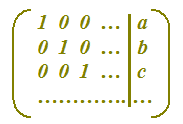
- a, b, c,.... rappresentano rispettivamente il valore della prima, della seconda, della terza, .... incognita.
Esempio.
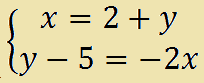
Scriviamo le equazioni in forma normale e mettiamo in ordine le incognite:
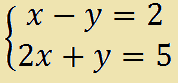
Scriviamo la matrice completa del sistema:
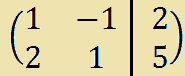
L'elemento della matrice situato sulla prima riga e sulla prima colonna è già uguale ad 1. Quindi eseguigiamo le seguenti trasformazioni:
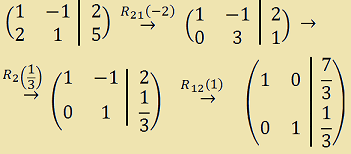
L'ultima matrice scritta è la matrice completa del seguente sistema:
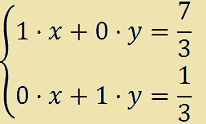
che equivale a dire
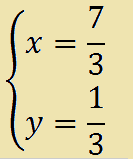
Abbiamo, quindi, trovato le soluzioni del sistema.
