SISTEMI DI EQUAZIONI LINEARI ALGEBRICHE
Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:
- Identità ed equazioni
- Espressioni algebriche
- Equazione di primo grado ad una incognita
- Sistemi di equazioni
- Risolvere un sistema di equazioni
In questa e nelle prossime lezioni parleremo di SISTEMI di EQUAZIONI LINEARI ALGEBRICHE.
Prima di procedere col trattare questo argomento ricordiamo che:
- un' EQUAZIONE è l'uguaglianza tra due espressioni letterali, che è verificata solo per particolari valori attribuiti alle sue lettere;
- le equazioni di primo grado sono dette anche EQUAZIONI LINEARI;
- un insieme di più equazioni che devono essere soddisfatte contemporaneamente prende il nome di SISTEMA DI EQUAZIONI.
Poste queste premesse vogliamo vedere come è possibile risolvere i SISTEMI DI EQUAZIONI LINEARI ALGEBRICHE del tipo:
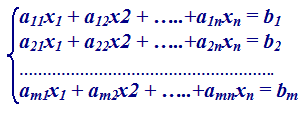
RISOLVERE un SISTEMA DI EQUAZIONI significa trovare le SOLUZIONI COMUNI a tutte le equazioni del sistema.
Ogni soluzione comune a tutte le equazioni del sistema si dice SOLUZIONE DEL SISTEMA.
Un sistema di equazioni potrà essere:
- IMPOSSIBILE se non esistono soluzioni che soddisfano contemporaneamente le equazioni del sistema;
- INDETERMINATO se esistono infinite soluzioni che soddisfano contemporaneamente le equazioni del sistema;
- DETERMINATO se le soluzioni che soddisfano contemporaneamente le equazioni del sistema sono in numero limitato.
Nelle prossime lezioni vedremo come è possibile risolvere tali sistemi.
