COME CALCOLARE IL RANGO DI UNA MATRICE
- Matrice
- Matrice identità
- Sottomatrice
- Determinante di una matrice quadrata
- Rango o caratteristica di una matrice
- Matrici equivalenti
- Matrice di forma canonica
- Riduzione a forma canonica di una matrice
- Calcolo del rango di una matrice
Vediamo come è possibile CALCOLARE il RANGO di una matrice A di ordine n x m.
Un primo metodo consiste nella RIDUZIONE a FORMA CANONICA della matrice data.
Torniamo all'esempio visto in una precedente lezione:
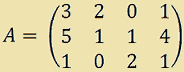
Ecco come appare la MATRICE una volta ridotta a FORMA CANONICA:
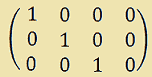
In pratica ci troviamo di fronte ad una forma canonica del tipo:
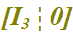
dove 3 è l'ordine della MATRICE IDENTITA'.
La riduzione a forma canonica, essendo ottenuta con delle operazioni elementari, ci porta ad avere una matrice EQUIVALENTE a quella data, cioè una matrice che ha lo stesso ordine e lo stesso rango della matrice A.
Il rango della matrice equivalente da noi ottenuta è uguale all'ORDINE della MATRICE IDENTITA', quindi nel nostro esempio esso è uguale a 3.
Infatti qualunque altra sottomatrice di ordine superiore conterebbe necessariamente una riga nulla e quindi il suo determinante sarebbe nullo.






