ALGORITMO DI KRONECKER
- Matrice
- Sottomatrice
- Determinante di una matrice quadrata
- Rango o caratteristica di una matrice
- Calcolo del rango di una matrice
- Come calcolare il rango di una matrice
L'ALGORITMO di KRONECKER consente di CALCOLARE il RANGO di una MATRICE riducendo il numero di determinanti che occorre calcolare.
Ricordiamo che
- il RANGO di una matrice A è il MASSIMO ORDINE dei MINORI aventi DETERMINANTE DIVERSO da ZERO;
- indichiamo il rango della matrice con r.
Ora prendiamo la matrice quadrata A di ordine 3 x 4:
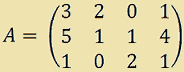
La nostra matrice potrebbe avare rango 0, oppure 1, oppure 2, oppure 3.
Iniziamo con l'estrarre, dalla matrice A, una sottomatrice quadrata di ordine 1, che chiameremo A', ad esempio:
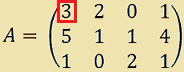
A' = (3).
Calcoliamo il determinante di questa sottomatrice e avremo:
det |3| = 3.
Il determinante di questa sottomatrice quadrata, che sappiamo prende anche il nome di minore, non è nullo. Quindi possiamo essere certi che il rango della nostra matrice sarà almeno uguale ad 1 dato che esiste un minore di ordine 1 con determinante non nullo.
Ora ORLIAMO la matrice A', cioèAGGIUNGIAMO alla matrice A' UNA RIGA e UNA COLONNA otterremo così la matrice A'' di ordine 2:
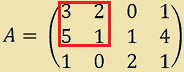
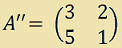
Calcoliamo il determinante di questa sottomatrice e avremo:
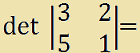
(3 · 1)-(2 · 5) = 3 - 10 = -7.
Il determinante di questa sottomatrice quadrata non è nullo. Quindi possiamo essere certi che il rango della nostra matrice sarà almeno uguale a 2 dato che esiste un minore di ordine 2 con determinante non nullo..
Ora ORLIAMO la matrice A'', cioèAGGIUNGIAMO alla matrice A'' UNA RIGA e UNA COLONNA otterremo così la matrice A''' di ordine 3:
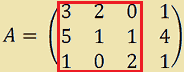
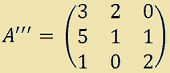
Calcoliamo il determinante di questa sottomatrice e avremo:
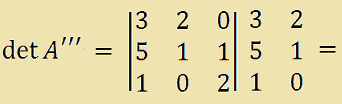
[(3 · 1 · 2) + (2 · 1 · 1) + (0 · 5 · 0)] +
- [(0 · 1 · 1) + (3 · 1 · 0) + (2 · 5 · 2)] =
[6 + 2 + 0] - [0 + 0 + 20] =
8 - 20 = -12.
Il determinante di questa sottomatrice quadrata non è nullo. Quindi possiamo essere certi che il rango della nostra matrice sarà 3 dato che esiste un minore di ordine 3 con determinante non nullo.
Quindi possiamo affermare che il rango della matrice A è 3.
Se la sottomatrice A''' avesse avuto determinante nullo, avremmo dovuto estrarre un'altra sottomatrice di ordine 3 per verificare che il suo determinante non fosse nullo e saremmo dovuti andare avanti a considerare tutte le sottomatrici di ordine 3.
Appena trovato un determinante non nullo da una sottomatrice di ordine 3 avremmo potuto dire che la matrice A ha rango 3. Se, invece il determinante di tutte le sottomatrici di ordine 3 fossero stati nulli avremmo affermato che il rango della matrice A è 2.
Ricapitolando il TEOREMA di KRONECKER afferma che:
- una matrice A ha rango r se, e solo se, ESISTE ALMENO UNA SOTTOMATRICE QUADRATA di A, che chiameremo A', di ORDINE r il cui DETERMINANTE è NON NULLO;
- le SOTTOMATRICI QUADRATE di A di ORDINE r+1 che si ottengono ORLANDO A' in tutti i modi possibili hanno DETERMINANTE NULLO.






