RIDUZIONE A FORMA CANONICA DI UNA MATRICE
In questa lezione vedremo come, partendo da una matrice A, è possibile ridurre tale matrice ai FORMA CANONICA.
Consideriamo la matrice A, il cui elemento a11 è diverso da zero e da 1. Cioè
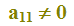
e
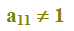
Esempio.
Consideriamo la matrice A
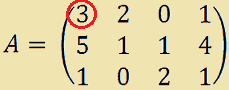
Come possiamo notare l'elemento a11 non è né zero, né uno: esso infatti è 3.
Ora dobbiamo ridurre tale elemento ad 1. Per fare questo moltiplichiamo gli elementi della prima riga per 1/3.
Quindi, generalizzando, per ridurre l'elemento a11 ad 1, MOLTIPLICHIAMO la PRIMA RIGA per 1/a11.
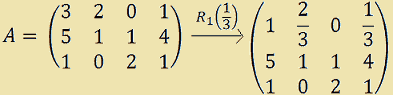
Ora dobbiamo applicare sulla matrice ottenuta una serie di trasformazioni in modo tale da RENDERE NULLI gli ELEMENTI della PRIMA COLONNA.
Quindi dobbiamo annullare:
- l'elemento 5 che si trova sulla seconda riga, prima colonna;
- l'elemento 1 che si trova sulla terza riga, prima colonna.
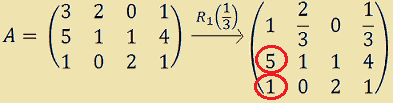
Per annullare questi due elementi proseguiamo in questo modo: iniziamo col sommare alla seconda riga, la prima moltiplicata per -5. Poiché il primo elemento della prima riga è 1, moltiplicandolo per -5, il prodotto è -5, che sommato a 5 dà zero.
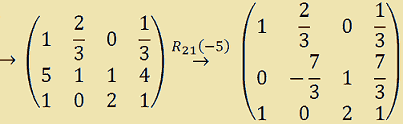
Ora annulliamo l'elemento 1 che si trova sulla terza riga prima colonna. Sarà necessario sommare alla terza riga la prima moltiplicata per -1. Poiché il primo elemento della prima riga è 1, moltiplicandolo per -1, il prodotto sarà -1, che sommato a 1 dà zero. Quindi avremo:
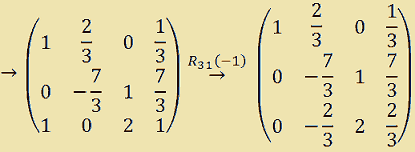
Quindi, generalizzando, per ridurre gli elementi ai1 (diversi dall'elemento a11) a 0, SOMMIAMO alla RIGA i la PRIMA RIGA MOLTIPLICATA per un valore k che è l'opposto dell'elemento da annullare.
Ora dobbiamo ridurre ad 1 l'elemento presente sulla seconda riga e seconda colonna, ovvero -7/3. Per fare questo moltiplichiamo la seconda riga per -3/7:
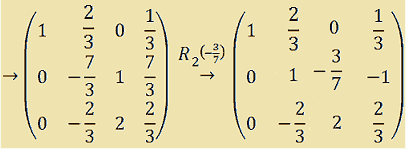
A questo punto annulliamo l'elemento 2/3 che si trova sulla prima riga seconda colonna. Per fare ciò sarà necessario sommare alla prima riga la seconda moltiplicata per -2/3.
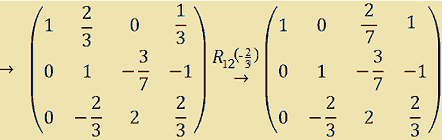
Poi annulleremo l'elemento -2/3 che si trova sulla terza riga seconda colonna sommando alla terza riga la seconda moltiplicata per 2/3.
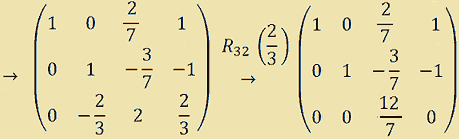
Continuiamo nel modo visto sopra. Avremo:
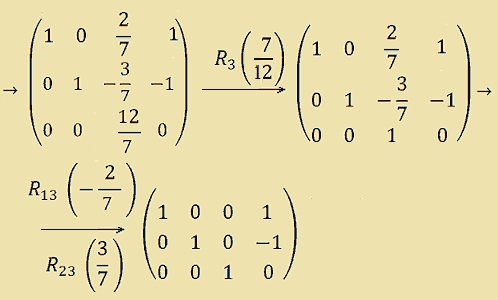
Nell'ultimo passaggio abbiamo eseguito le due trasformazioni indicate in una sola volta.
Ora, per ridurre la matrice a forma canonica dobbiamo annullare gli elementi della quarta colonna: per farlo operiamo due trasformazioni sulle colonne.
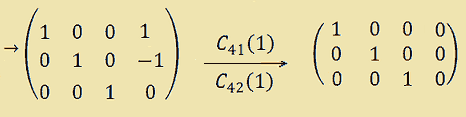
Come si può notare abbiamo ridotto la nostra matrice A a forma canonica ottenendo una matrice del tipo:
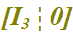
Nella prossima lezione faremo ancora alcune considerazioni sulla RIDUZIONE a FORMA CANONICA delle MATRICI.






