MATRICI EQUIVALENTI
Ipotizziamo di avere due matrici
A e B.
Esse si dicono EQUIVALENTI quando hanno:
- lo stesso ORDINE;
- lo stesso RANGO.
Chiamiamo OPERAZIONI ELEMENTARI alcune trasformazioni che, se applicate ad una matrice, portano ad ottenere una MATRICE EQUIVALENTE a quella data, cioè non mutano né l'ordine, né il rango della matrice data.
Sono OPERAZIONI ELEMENTARI:
- SCAMBIARE tra loro DUE RIGHE o DUE COLONNE;
- MOLTIPLICARE gli elementi di UNA RIGA o di UNA COLONNA per un NUMERO DIVERSO da ZERO;
- SOMMARE agli elementi di UNA RIGA i CORRISPONDENTI elementi di un'altra riga MOLTIPLICATI per un NUMERO o SOMMARE agli elementi di UNA COLONNA i CORRISPONDENTI elementi di un'altra colonna MOLTIPLICATI per un NUMERO.
Indichiamo le OPERAZIONI ELEMENTARI appena viste con i seguenti simboli:
Rij Indica lo scambio
della i-esima riga con la j-esima riga.
Cij
Indica lo scambio
della i-esima colonna con la j-esima colonna.
Ri(k)
Indica la moltiplicazione
degli elementi della i-esima riga per il numero k diverso
da zero.
Ci(k)
Indica la moltiplicazione
degli elementi della i-esima colonna per il numero k
diverso da zero.
Rij(k)
Indica la somma degli
elementi della i-esima riga con i corrispondenti elementi
della j-esima riga moltiplicati per il numero k.
Cij(k)
Indica la somma degli
elementi della i-esima colonna con i corrispondenti elementi
della j-esima colonna moltiplicati per il numero k.
Esempio.
Partiamo dalla matrice A
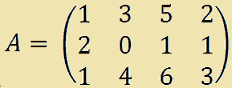
ed applichiamo le seguenti operazioni elementari nell'ordine dato:
- scambiamo la prima riga con la terza riga;
- moltiplichiamo la seconda colonna per 3;
- sommiamo agli elementi della seconda riga, gli elementi della prima riga moltiplicati per 2.
Avremo:
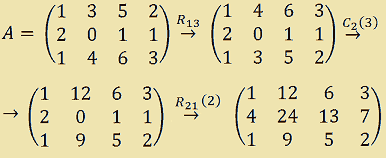
La matrice ottenuta è una matrice equivalente a quella data.
Le matrici ottenibili l'una dall'altra attraverso delle OPERAZIONI ELEMENTARI per RIGA si dicono MATRICI EQUIVALENTI per RIGA.






