LUNGHEZZA DI UN ARCO
- Lunghezza della circonferenza
- La circonferenza e il cerchio
- Corde di una circonferenza
- Il segmento
- Archi di una circonferenza
- Angoli al centro
Dallo studio della circonferenza abbiamo appreso che, si chiama CORDA un SEGMENTO che UNISCE DUE PUNTI QUALSIASI di una CIRCONFERENZA.
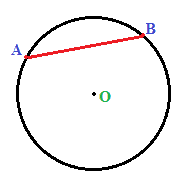
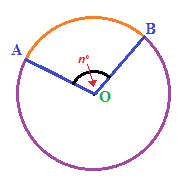
Sappiamo anche che il segmento AB divide la circonferenza in due archi che, nella figura sottostante abbiamo indicato uno in arancio e l'altro in viola:
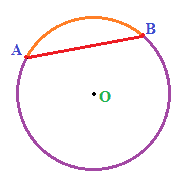
Ora noi sappiamo che l'AMPIEZZA dell'ARCO
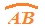
che si legge
arco AB
cioè l'ampiezza dell'arco che, nell'immagine sopra, abbiamo indicato in arancio, è la misura in gradi del suo CORRISPONDENTE ANGOLO AL CENTRO:
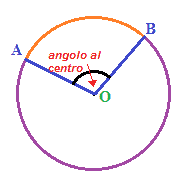
Possiamo considerare una circonferenza come un arco il cui corrispondente angolo al centro misura 360°.
Al tempo stesso possiamo immaginare la circonferenza divisa in 360 parti uguali, ad ognuna delle quali corrisponderà un angolo al centro di 1°.
Di conseguenza la lunghezza di un arco lungo 1° è pari alla trecento sessantesima parte della circonferenza, cioè:
lunghezza dell'arco ampio 1° = C/ 360.
Ma noi sappiamo che la lunghezza della circonferenza è uguale a:
C = 2π x r.
Quindi possiamo scrivere:
lunghezza dell'arco ampio 1° =
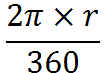
Se l'arco è di 2° la sua lunghezza sarà il doppio della lunghezza dell'arco ampio 1°, cioè:
lunghezza dell'arco ampio 2° =
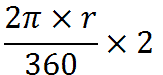
Se l'arco è di 3° la sua lunghezza sarà il triplo della lunghezza dell'arco ampio 1°, cioè:
lunghezza dell'arco ampio 3° =
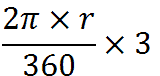
Se l'arco è di n°
la sua lunghezza sarà n volte la lunghezza dell'arco ampio 1°, cioè:
lunghezza dell'arco ampio n° =
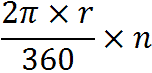
Quindi possiamo dire che la LUNGHEZZA DI UN ARCO di circonferenza si ottiene DIVIDENDO la LUNGHEZZA della CIRCONFERENZA per 360° e MOLTIPLICANDO il risultato ottenuto per l'AMPIEZZA DELL'ARCO espressa in gradi. Ovvero:
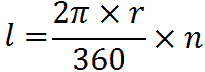
Esempio:
calcolare la lunghezza di un arco di una circonferenza sapendo che la sua ampiezza è di 36° e che il raggio della circonferenza misura cm 4.
Applichiamo la formula precedente e abbiamo
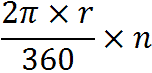
[(2 x 3,14 x 4)/ 360] x 36 = (25,12/ 360) x 36 = 2,51 cm.
La lunghezza dell'arco è pari a 2,51 cm.






