DOMINIO DI UNA FUNZIONE TRIGONOMETRICA
- Funzioni reali di variabile reale
- Classificazione delle funzioni reali
- L'insieme dei numeri reali
- L'insieme dei numeri razionali relativi
Si chiamano FUNZIONI TRIGONOMETRICHE o GONIOMETRICHE quelle funzioni nelle quali compaiono il seno, il coseno, la tangente, ecc.. della variabile x.
Il CAMPO DI ESISTENZA di queste funzioni è diverso a seconda del tipo di funzione. Vediamo di seguito le principali funzioni trigonometriche e i loro rispettivi campi di esistenza.
Nelle funzioni del tipo
y = sin x
che si legge
y è uguale al seno di x
il CAMPO DI ESISTENZA è dato da QUALSIASI x appartenente ai REALI.
Nelle funzioni del tipo
y = cos x
che si legge
y è uguale al coseno di x
il CAMPO DI ESISTENZA è dato da QUALSIASI x appartenente ai REALI.
Ora esaminiamo una funzione del tipo:
y = tg x
che si legge
y è uguale alla tangente di x.
Sappiamo che la tangente di x è data dal RAPPORTO tra il seno di x e il coseno di x. Inoltre sappiamo che in una funzione fratta, per trovare il campo di esistenza, dobbiamo porre il denominatore diverso da zero.
Quindi:
y = tg x = sen x/ cos x
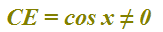
Ma il coseno di x è uguale a zero quando
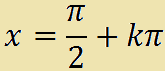
che si legge
x è uguale a pi-greco mezzi più k pi-greco.
Quindi il CAMPO DI ESISTENZA della funzione sarà:
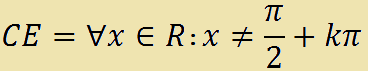
che si legge
campo di esistenza uguale a qualunque x appartenente ad R tale che x è diverso da pi-greco mezzi più k pi-greco.
Sottolineiamo che k è un numero appartenente all'insieme Z dei NUMERI INTERI.
Ora consideriamo la funzione:
y = ctg x
che si legge
y è uguale alla cotangente di x.
Sappiamo che la cotangente di x è data dal RAPPORTO tra il coseno di x e il senodi x. Inoltre sappiamo che in una funzione fratta, per trovare il campo di esistenza, dobbiamo porre il denominatore diverso da zero.
Quindi:
y = ctg x = cos x/ sen x

Ma il seno di x è uguale a zero quando
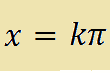
che si legge
x è uguale a k pi-greco.
Quindi il CAMPO DI ESISTENZA della funzione sarà:
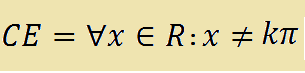
che si legge
campo di esistenza uguale a qualunque x appartenente ad R tale che x è diverso da k pi-greco.
Anche in questo caso k è un numero appartenente all'insieme Z dei NUMERI INTERI.
Infine, nel caso in cui la funzione trigonometrica fosse una delle seguenti
y = arcsin x
y = arccos x
il campo di esistenza è dato dalle
-1 ≤ x ≤ +1.






