RISOLUZIONE DELLE EQUAZIONI ESPONENZIALI MEDIANTE SOSTITUZIONE
- Funzione esponenziale
- Risoluzione delle equazioni di secondo grado complete
- Risoluzione di equazioni esponenziali
- Equazione esponenziale elementare
- Risoluzione di equazioni esponenziali con potenze della stessa base
- Risoluzione di equazioni esponenziali con potenze aventi lo stesso esponente
- Risoluzione di equazioni esponenziali con potenze aventi basi ed esponenti diversi
- Risoluzione delle equazioni esponenziali con metodo grafico
Proseguiamo l'esame dei metodi di risoluzione delle equazioni esponenziali vedendo il caso in cui l'equazione si presenta nella forma
a·d 2f(x) + b·d f(x) + c = 0 .
Questo tipo di equazioni si risolve mediante SOSTITUZIONE ponendo
d f(x) = z.
In questo modo l'equazione diventa
az2 + bz + c = 0
che si risolve come una normale equazione di secondo grado.
Una volta trovate le soluzioni esse andranno sostituite al posto di z.
Esempio 1:
4x-1 - 2x-1 +1/4 = 0 .
Scriviamo il 4 sotto forma di potenza ed abbiamo:
22(x - 2x-1 +1/4 = 0.
Poniamo
2x-1 = z
e sostituiamo nella precedente
22(x - 2x-1 +1/4 = 0.
z2 - z +1/4 = 0.
Risolviamo come una normale equazione di secondo grado:
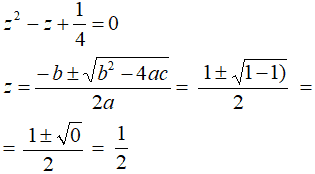
Ora, poiché
2x-1 = z
e
z = 1/2
poniamo
2x-1= 1/2
che possiamo scrivere come
2x-1 = 2-1.
Abbiamo così ottenuto un'equazione esponenziale che ha, a primo e secondo membro, due potenze aventi la stessa base. Essa si risolve uguagliando gli esponenti. Ovvero:
x -1 = -1
da cui ricaviamo
x = -1 + 1 = 0
x = 0.






