COORDINATE DEL PUNTO MEDIO DI UN SEGMENTO
- Assi cartesiani ortogonali
- Rappresentazione di un punto su un pianto cartesiano
- Rappresentazione di un punto su un pianto cartesiano: alcuni esempi
- Rappresentazione di un punto su un pianto cartesiano: casi particolari
- Il punto
- Il segmento
- Minimo comune denominatore
Supponiamo di avere due punti A e B tali che:
A (x1 ; y1)
e
B (x2 ; y1).
In altre parole, i due punti, hanno la STESSA ORDINATA.
Disegniamo i due punti sugli assi cartesiani:
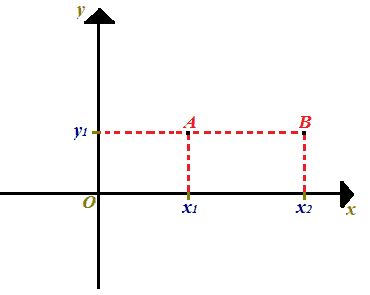
Ora, vogliamo determinare il PUNTO MEDIO DEL SEGMENTO AB:
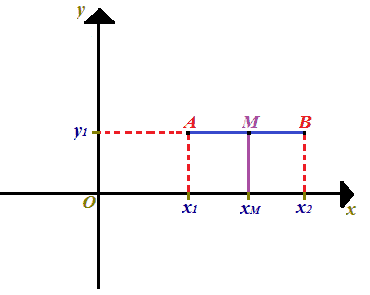
Poiché i punti A e B hanno la STESSA ORDINATA, anche il punto M avrà la STESSA ORDINATA. Si tratterà, allora, di trovare solamente l'ascissa del punto M che, nel grafico precedente abbiamo indicato con xM.
Osserviamo che per trovare l'ascissa xM dobbiamo trovare la misura del segmento OM' che sugli assi cartesiani, riportati sotto, abbiamo evidenziato in verde. Inoltre, sull'asse delle ascisse abbiamo indicato con A', M' e B' le proiezioni dei punti A, M e B sull'asse delle x:
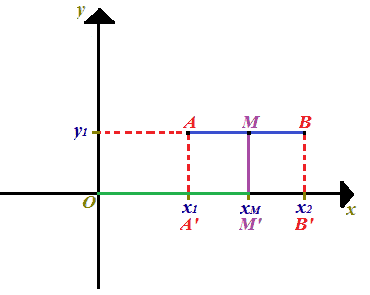
Ora notiamo che il segmento OM' è dato dal segmento OA' più il segmento A'M'. Ovvero:
OM' = OA' + A'M'.
Ma sappiamo che A'M' è uguale alla metà del segmento A'B', dato che M' è il punto medio del segmento AB. Quindi possiamo scrivere:
OM' = OA' + A'B'/2.
Essendo:
- OA' = x1
- A'B'
= x2 - x1
con x2 > x1
possiamo scrivere:
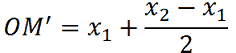
da cui, trovando il minimo comune denominatore, che è 2, otteniamo
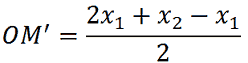
ed eseguendo, a numeratore, la differenza tra 2x1 ed x1, otteniamo:
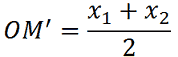
Quindi, nel caso di DUE PUNTI aventi la stessa ordinata,il PUNTO MEDIO ha:
-
come ascissa la SOMMA delle ASCISSE dei due punti, DIVISO 2;
- come ordinata, l'ORDINATA dei due punti.
Esempio:
dati i punti A (-2; 2) e B (0; 2) calcolare il punto medio.
Disegniamo i due punti:
I due punti hanno la stessa ordinata. Ora andiamo a calcolare il punto medio:
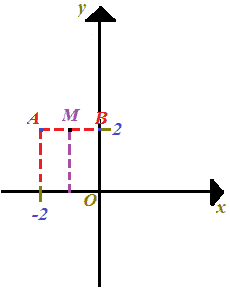
OM' = (x1 + x2) /2 = (-2 + 0)/ 2 = -2/2 = -1.
Il punto medio M ha come coordinate
M (-1; 2).






