CIRCONFERENZE E RETTE
- La circonferenza e il cerchio
- Posizioni di una retta rispetto ad una circonferenza
- Il punto
- La retta
- Triangoli
- Triangolo rettangolo
- Angolo retto - angolo acuto - angolo ottuso
- Figure geometriche equivalenti e figure geometriche congruenti
Disegniamo una CIRCONFERENZA e un PUNTO P ESTERNO ad essa:

Ora disegniamole due rette passanti per P e TANGENTI alla circonferenza rispettivamente nei punti H e K:
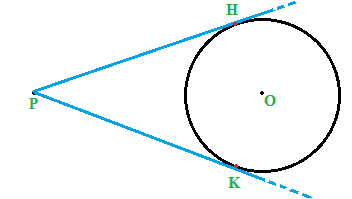
Disegniamo ora i due raggi OH e OK e la retta passante per i punti P e O. Avremo:
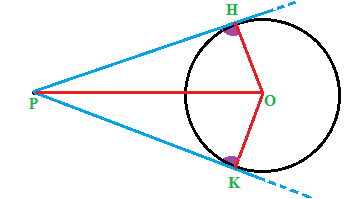
I due TRIANGOLI ottenuti POH e OPK sono due TRIANGOLI RETTANGOLI: l'angolo retto lo abbiamo evidenziato nell'immagine con il colore viola.
Se proviamo a sovrapporre i due triangoli, piegando la figura lungo il lato comune OP noteremo che essi sono CONGRUENTI.
Di conseguenza anche PH e PK sono CONGRUENTI. Quindi possiamo scrivere:
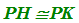
che si legge
PH è congruo a PK.
Quindi si può affermare che le TANGENTI condotte a una CIRCONFERENZA da un punto P ESTERNO ad essa individuano due segmenti, limitati dal punto P e dai punti di tangenza, CONGRUENTI tra loro.






