COME SI ESEGUE LA DIVISIONE TRA DUE POLINOMI

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• I polinomi
• Quoziente di monomi
• Divisione
• Somma algebrica di numeri relativi
• Polinomi ordinati

Nella lezione precedente abbiamo visto come, dati due polinomi, A e B divisibili tra loro, il loro quoziente è un terzo polinomio Q tale che, moltiplicando Q per B otteniamo A.

Quindi:

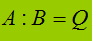
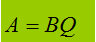
Se invece A e B non sono divisibili tra loro avremo:

Ora vediamo come possiamo determinare, concretamente il valore di Q, ed eventualmente, il valore di R.

Immaginiamo di voler eseguire la seguente divisione:

(x³ + 2x² -9x -4) : (x² -2x - 1).

1. Per prima cosa i due polinomi devono essere ORDINATI secondo le POTENZE DECRESCENTI di una STESSA LETTERA.

   Nel nostro esempio, i due polinomi sono già ordinati secondo le potenze decrescenti di x.

   Scriviamo la nostra divisione come di consueto:

   
   
   

2. DIVIDIAMO il PRIMO TERMINE del DIVIDENDO (x³) per il PRIMO TERMINE del DIVISORE (x²). Il risultato ottenuto (x) lo scriviamo sotto il divisore: esso rappresenta il PRIMO TERMINE del nostro QUOZIENTE.

   
   
   

3. MOLTIPLICHIAMO il PRIMO TERMINE del nostro QUOZIENTE (x) per il DIVISORE (x² - 2x -1). Il risultato ottenuto (x³ - 2x² -x) prende il nome di PRIMO PRODOTTO PARZIALE.

   SOTTRAIAMO il PRIMO PRODOTTO PARZIALE dal DIVIDENDO ed otteniamo il PRIMO RESTO PARZIALE.

   Per rendere più agevole l'operazione, mano a mano che otteniamo i vari termini del prodotto parziale, lo scriviamo sotto al dividendo con il segno cambiato e successivamente si esegue la somma algebrica.

   
   
   

4. DIVIDIAMO il PRIMO TERMINE del primo RESTO PARZIALE (4x²) per il PRIMO TERMINE del DIVISORE (x²). Il risultato ottenuto (4) lo scriviamo sotto il divisore, a fianco del primo termine del quoziente (x): esso rappresenta il SECONDO TERMINE del nostro QUOZIENTE.

   
   
   

5. MOLTIPLICHIAMO il SECONDO TERMINE del nostro QUOZIENTE (4) per il DIVISORE (x² - 2x -1). Il risultato ottenuto (4x² - 8x -4) prende il nome di SECONDO PRODOTTO PARZIALE.

   SOTTRAIAMO il SECONDO PRODOTTO PARZIALE dal PRIMO RESTO PARZIALE ed otteniamo il SECONDO RESTO PARZIALE.

   Anche in questo caso per rendere più agevole l'operazione, mano a mano che otteniamo i vari termini del prodotto parziale, lo scriviamo sotto al dividendo con il segno cambiato e successivamente eseguiamo la somma algebrica.

   
   
   

6. Si continua così fino a quando non si giunge ad un resto parziale nullo o a un polinomio di grado minore rispetto a quello del divisore.
   

   LA LEZIONE PROSEGUE SOTTO LA PUBBLICITA'

   Pubblicità/Advertising

   Nel nostro esempio abbiamo ottenuto un resto uguale a zero, quindi possiamo scrivere:

   (x³ + 2x² -9x -4) : (x² -2x - 1) = x + 4.

Vediamo un altro esempio:

(6x³ - 2x² +3x -1) : (2x² +1) .

In questo caso possiamo notare che, il divisore non è un POLINOMIO COMPLETO.

Infatti, nel divisore manca il termine con lettera x.

Quando il DIVIDENDO o il DIVISORE e entrambi, non sono POLINOMI COMPLETI, conviene scriverli lasciando degli spazi vuoti in corrispondenza dei termini mancanti. Così:

E successivamente procedere come di consueto:

Quindi scriveremo:

(6x³ - 2x² +3x -1) : (2x² +1) = 3x - 1.

Concludiamo con un ultimo esempio:

(x² +4x +2) : (x +1).

Avremo:

In questo caso i due polinomi non sono divisibili tra loro è abbiamo un quoziente incompleto e un resto:

(x² +4x +2) : (x +1) = x+3 con resto di -1.

Per approfondire questo argomento, leggi:

• Grado del quoziente tra un polinomio e un monomio

Lezione precedente - Lezione successiva

Indice degli argomenti sui polinomi

Pubblicità/Advertising