DIVISIONE DI DUE POLINOMI
Immaginiamo di avere due polinomi. Li chiamiamo rispettivamente A e B.
Supponiamo, inoltre che B sia diverso da zero.
Il polinomio A è divisibile per il polinomio B quando esiste un terzo polinomio, Q tale che, moltiplicando Q per B otteniamo A.
Quindi:
dati: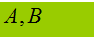
con
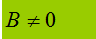
si legge
B diverso da zero
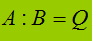
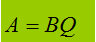
Ricordiamo che:
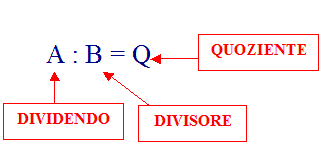
Quindi, un POLINOMIO si dice DIVISIBILE per un secondo POLINOMIO se esiste un terzo POLINOMIO che MOLTIPLICATO PER IL SECONDO, dà come prodotto il PRIMO.
Quando il POLINOMIO A non è divisibile per iL POLINOMIO B, il QUOZIENTE può essere indicato come una frazione che ha al NUMERATORE il DIVIDENDO e al DENOMINATORE il DIVISORE. Tale frazione prende il nome di frazione algebrica.
Tuttavia se il GRADO del POLINOMIO A rispetto ad una data lettera è maggiore o uguale a quella di B
possiamo trovare altri due polinomi Q e R, tali che:
In questo caso Q prende il nome di QUOZIENTE INCOMPLETO o più semplicemente QUOZIENTE, mentre R è il RESTO della divisione.
Invece, se il POLINOMIO A è divisibile per il POLINOMIO B, Q prende il nome di QUOZIENTE COMPLETO ed ovviamente il RESTO R, sarà uguale a zero.
Quindi:
con
R = 0
Q = quoziente completo
R diverso da 0
Q = quoziente incompleto
Nella prossima lezione vedremo come è possibile eseguire la DIVISIONE tra due POLINOMI.






