GRADO DI UN MONOMIO
- I monomi
- Monomi interi e frazionari
- Monomi simili, uguali, opposti
- Casi particolari dell'elevazione a potenza
In questa lezione prenderemo in esame solamente MONOMI INTERI, cioè monomi le cui LETTERE figurano esclusivamente a NUMERATORE.
Ad esempio
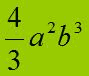
è un MONOMIO INTERO dato che le LETTERE vi compaiono solo a NUMERATORE e con ESPONENTE POSITIVO.
Dato un MONOMIO INTERO si dice GRADO COMPLESSIVO del monomio la SOMMA DEGLI ESPONENTI delle sue LETTERE.
Torniamo al monomio precedente
4/3a2b3.
Avremo
- Monomio: 4/3a2b3
- Parte letterale del monomio: a2b3
- Esponente della lettera a: 2
- Esponente della lettera b 3
- Somma degli esponenti delle lettere 2+3 = 5
- Grado complessivo monomio 5
Quindi il GRADO COMPLESSIVO del nostro monomio è 5.
Vediamo un altro esempio:
5x2y5z.
La prima cosa che dobbiamo osservare è che la lettera z non ha esponente.
ATTENZIONE!!! Quando una LETTERA è PRIVA DI ESPONENTE va considerata come una potenza avente ESPONENTE 1.
Quindi avremo:
- Monomio: 5x2y5z
- Parte letterale del monomio: x2y5z
- Esponente della lettera x: 2
- Esponente della lettera y: 5
- Esponente della lettera z: 1
- Somma degli esponenti delle lettere: 2+5+1 = 8
- Grado complessivo monomio: 8
Quindi il GRADO COMPLESSIVO del nostro monomio è 8.
Oltre al grado complessivo di un monomio possiamo definire anche il GRADO DI UN MONOMIO RISPETTO AD UNA SUA LETTERA.
Il GRADO DI UN MONOMIO INTERO RISPETTO ad una sua LETTERA è l'ESPONENTE DI QUELLA LETTERA.
Ad esempio:
se vogliamo sapere il grado del monomio
5x2y5z
rispetto alla lettera x, esso è 2, cioè l'esponente con il quale tale lettera compare nel monomio.
ATTENZIONE!!! Se in un monomio MANCA una certa LETTERA, si dice che quel MONOMIO è di GRADO ZERO rispetto a QUELLA LETTERA.
Esempio:
4a2
è un monomio di grado zero rispetto alla lettera b. Infatti possiamo immaginare di scrivere il monomio nel modo seguente:
4a2b0.
E come sappiamo qualsiasi numero elevato a zero è uguale a 1. Quindi sarebbe come scrivere:
4 x a2 x 1.
Di conseguenza anche +5, o -3 sono monomi: essi sono MONOMI DI GRADO ZERO.
Infatti li possiamo immaginare scritti come:
+5a0= +5
-3x0= -3.
Ricapitolando:
GRADO COMPLESSIVO DI UN MONOMIO:
- SOMMA DEGLI ESPONENTI DELLE SUE LETTERE
- Esempio:
+4a2b
grado 2+1 =3
GRADO DEL MONOMIO RISPETTO AD UNA LETTERA:
- ESPONENTE DI QUELLA LETTERA
- Esempio:
+4a2b
grado del monomio rispetto alla lettera a = 2
- Esercizio 8 - Grado complessivo di un monomio
- Esercizio 9 - Grado complessivo di un monomio
- Esercizio 10 - Grado di un monomio rispetto ad una lettera
- Esercizio 11 - Grado complessivo di un monomio






