I MONOMI
- Monomi interi e monomi frazionari
- Monomi simili, uguali e opposti
- Grado di un monomio
- Proprietà delle potenze
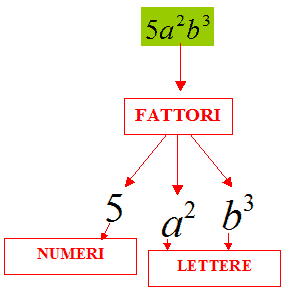
Un MONOMIO è il PRODOTTO di più FATTORI rappresentati da NUMERI e LETTERE.
Ad esempio:

sono tre monomi.
Infatti:


Nei monomi, quindi, non compaiono MAI i segni dell'ADDIZIONE e/o della SOTTRAZIONE.
Ad esempio
non sono monomi perché in essi compaiono i segni dell'addizione e della sottrazione come abbiamo evidenziato nell'immagine sottostante.


Invece

è un monomio.
Infatti, se moltiplichiamo tra loro i fattori numerici (+2) e (-3) abbiamo
 .
.
Successivamente moltiplichiamo i fattori letterali che hanno la stessa base, ovvero a. Il prodotto di due potenze aventi la stessa base e una potenza avente la stessa base e con esponente uguale alla somma degli esponenti: quindi a per a è uguale ad a alla seconda.

Quello che abbiamo adesso è un monomio esattamente come quelli che abbiamo visto prima.
Questo MONOMIO si dice RIDOTTO A FORMA NORMALE.
Possiamo affermare, quindi, che un monomio si dice ridotto a forma normale quando assume la sua forma tipica che è quella del prodotto tra un solo fattore numerico e di fattori letterali, in cui ciascuna lettera compare una sola volta elevata ad un certo esponente.

In un monomio ridotto a forma normale, chiamiamo:
- COEFFICIENTE il FATTORE NUMERICO;
- PARTE LETTERALE il prodotto dei FATTORI LETTERALI COI LORO ESPONENTI.
Esempio:
- MONOMIO: +3 a2b
- COEFFICIENTE: a2b
- PARTE LETTERALE: a2b
Esempio:
- MONOMIO: -5x3y2
- COEFFICIENTE: -5
- PARTE LETTERALE: x3y2
Esempio:
- MONOMIO: -1/3ab2c
- COEFFICIENTE: -1/3
- PARTE LETTERALE: ab2c
Si chiama MONOMIO NULLO il monomio che ha per COEFFICIENTE lo ZERO.
Infatti, moltiplicando per zero la parte letterale, il risultato è zero.

Si chiama SEGNO DEL MONOMIO il SEGNO DEL COEFFICIENTE del monomio.
MONOMIO: +4ab
SEGNO DEL MONOMIO: +
MONOMIO: -5a
SEGNO DEL MONOMIO: -
Il segno + davanti ad un monomio può essere tralasciato. Ad esempio possiamo scrivere indifferentemente:
+3a
oppure
3a.
Se il monomio ha coefficiente 1, esso si può tralasciare. Ad esempio possiamo scrivere:
+1a
oppure
+a
oppure, potendo tralasciare anche il segno +
a
-1a
oppure
-a
in questo caso il segno deve essere sempre indicato, poiché esso è -
- Esercizio 1 - I monomi
- Esercizio 2 - Coefficiente e parte letterale di un monomio
- Esercizio 3 - Coefficiente e parte letterale di un monomio






