POTENZE DI NUMERI RELATIVI
- L'insieme dei numeri interi
- L'insieme dei numeri naturali
- Simboli usati per l'insieme dei numeri interi
- Potenze di numeri relativi
- Elevamento a potenza
- I numeri relativi
Nella lezione precedente, parlando della potenza di numeri interi relativi, abbiamo detto che l'elevamento a potenza è UN'OPERAZIONE INTERNA in Z*.
Ora esaminiamo un po' meglio l'operazione di ELEVAMENTO A POTENZA di un NUMERO INTERO RELATIVO.
Supponiamo di dover eseguire:
an
che si legge
a elevato ad n
posto che:
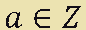
che si legge
a appartiene a Z
e che
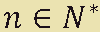
che si legge
n appartiene a N.
Ricordiamo che si chiama VALORE ASSOLUTO, il numero relativo preso senza il suo segno.
Il valore assoluto di un numero relativo si indica mettendo il numero tra due stanghette verticali.
Quindi, indicheremo il valore assoluto di a nel modo seguente:
|a|
che si legge
valore assoluto di a.
Fatte queste premesse possiamo dire che, se a è un NUMERO INTERO POSITIVO,
an = |a|n.
In altre parole se a è un numero intero positivo, quindi se è MAGGIORE DI ZERO, an è uguale al valore assoluto di a elevato ad n, cioè è uguale ad a preso senza il suo segno elevato ad n.
Esempi:
Infatti:42 = |+4|2 = 42
(+4)·(+4) = +16
e
4·4 = +16
+53 = |+5|3 = 53
(+5)·(+5)·(+5) = +125
e
5·5·5 = +125
+104 = |+10|4 = 104
(+10)·(+10)·(+10)·(+10) = +10.000
e
10·10·10·10 = 10.000
Se invece a è un NUMERO INTERO NEGATIVO occorre distinguere due ipotesi. La prima ipotesi è che n è PARI. Anche in questo caso
an = |a|n.
In altre parole se a è un numero intero negativo, quindi se è MINORE DI ZERO, e allo stesso tempo n è PARI,an è uguale al valore assoluto di a elevato ad n, cioè è uguale ad a preso senza il suo segno elevato ad n.
Esempi:
Infatti:-52 = |-5|2 = 52
(-5)·(-5) = +25
e
5·5 = +25
-44 = |-4|4 = 44
(-4)·(-4)·(-4)·(-4) = +256
e
4·4·4·4 = +256
-26 = |-2|6 = 26
(-2)·(-2)·(-2)·(-2)·(-2)·(-2) = +64
e
2·2·2·2·2·2
= +64
Infine se a è sempre un NUMERO INTERO NEGATIVO, ma n è DISPARI, avremo:
an = -|a|n.
In altre parole se a è un numero intero negativo, quindi se è MINORE DI ZERO, e allo stesso tempo n è DISPARI,an è uguale all'opposto del valore assoluto.
Esempi:
Infatti:(-6)1
|-6|1 = 61
-|-6|1 = -61
(-6) = -6
(-4)3
|-4|3 = 43
-|-4|3 = -43
(-4)·(-4)·(-4)
= -64
(-2)5
|-2|5 = 25
-|-2|5 = -25
(-2)·(-2)·(-2)·(-2)·(-2)
= -32
Quindi, ricapitolando, possiamo dire che:
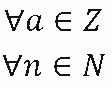
che si legge
per qualunque a appartenente a Z e per qualunque n appartenente ad N
an =|a|n
Se a > 0
an =|a|n
Se a < 0 ed n
pari
an = - |a|n
Se a < 0 ed n dispari






