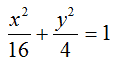EQUAZIONE DELL'ELLISSE DATI I DUE VERTICI
- L'ellisse
- Equazione dell'ellisse con centro nell'origine e fuochi sull'asse delle x
- Equazione dell'ellisse con centro nell'origine e fuochi sull'asse delle y
- Disegnare un'ellisse
Vediamo come si risolvono i problemi nei quali viene chiesto di SCRIVERE l'EQUAZIONE di un'ELLISSE quando sono note le coordinate:
- di uno dei VERTICI situati sull'asse delle ascisse
- e di uno dei VERTICI situati sull'asse delle ordinate.
Esempio:
scrivere l'equazione canonica dell'ellisse aventi i vertici
V1
(4; 0)
V2
(0; 2).
Come è evidente, il vertice V1 è situato sull'asse delle ascisse, mentre il vertice V2 è situato sull'asse delle ordinate.
Noi sappiamo che il VERTICE dell'ELLISSE situato sull'ASSE DELLE ASCISSE ha coordinate:
V1 (a; 0)
mentre il VERTICE dell'ELLISSE situato sull'asse delle ordinate ha coordinate:
V2 (0; b).
L'equazione canonica dell'ellisse è del tipo:
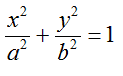
Dato che nel nostro caso:
a = 4
e
b = 2
avremo che:
a2 = 16
e
b2 = 4.
Quindi la nostra equazione sarà: