AREA DI UN POLIGONO CIRCOSCRITTO
- I poligoni
- La circonferenza e il cerchio
- Posizioni di una retta rispetto ad una circonferenza
- Poligoni circoscritti
- Poligoni equivalenti
- Area del triangolo
Disegniamo un POLIGONO i cui LATI siano TUTTI TANGENTI ad una CIRCONFERENZA di centro O e di raggio r:
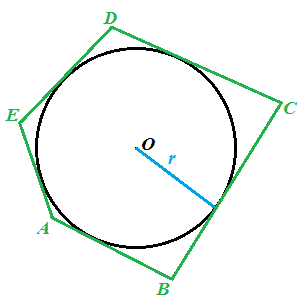
Come sappiamo questo POLIGONO si dice CIRCOSCRITTO alla circonferenza.
Ora congiungiamo i vertici del poligono con il centro del cerchio O: abbiamo così scomposto il poligono in 5 TRIANGOLI
Abbiamo chiamato tali triangoli, rispettivamente, T1, T2, T3, T4, T5:
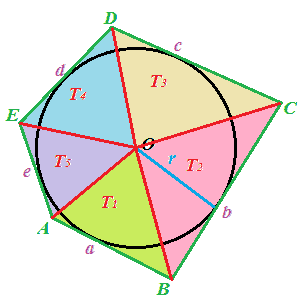
I 5 triangoli da noi disegnati hanno come basi, rispettivamente, i lati a, b, c, d, e. L'altezza di ogni triangolo è il raggio del cerchio r.
I 5 triangoli sono equivalenti ad un triangolo avente per base la somma delle basi e per altezza il raggio r. Inoltre, poiché ogni triangolo ha per base un lato del poligono, la somma delle basi non è altro che il perimetro del poligono.
Possiamo allora dire che un POLIGONO CIRCOSCRITTO ad un CERCHIO è EQUIVALENTE ad un TRIANGOLO avente:
- per BASE il PERIMETRO del poligono;
- per ALTEZZA il RAGGIO del cerchio.
Noi sappiamo che l'area del triangolo è uguale a:
A = (b x h)/2
dove
A = area
b = base
h = altezza.
Poiché nel nostro caso la base è uguale al perimetro e l'altezza è uguale al raggio del cerchio, possiamo dire che l'AREA del POLIGONO CIRCOSCRITTO è data da:
A = (P x r)/ 2
dove
A = area
P = perimetro del poligono
r = raggio del cerchio.
Da questa formula possiamo ricavare anche le formule inverse:
r = (A x 2)/ P
P
= (A x 2)/ r.
Esempio 1:
Un quadrilatero circoscritto ad una circonferenza avente il raggio lungo cm 4, ha il perimetro di cm 40. Calcolare la sua area.
Per risolvere il problema è sufficiente applicare la formula relativa al calcolo dell'area:
A = (P x r)/ 2 = (40 x 4)/ 2 = 160/ 2 = 80 cm2.
Esempio 2:
Un poligono circoscritto ad una circonferenza ha l'area di cm2 120. Sapendo che il raggio della circonferenza misura cm 8, determinare il perimetro del poligono.
Applichiamo la formula inversa e abbiamo:
P = (A x 2)/ r = (120 x 2)/ 8 = 30 cm.






