SIMMETRIA CENTRALE E ROTAZIONE
Nelle lezioni precedenti abbiamo parlato di simmetrie centrali. Ora andiamo a vedere il rapporto che esiste tra simmetria centrale e rotazione.
Disegniamo la figura F ed un punto O.

Costruiamo la figura F' simmetrica di F rispetto al punto O.
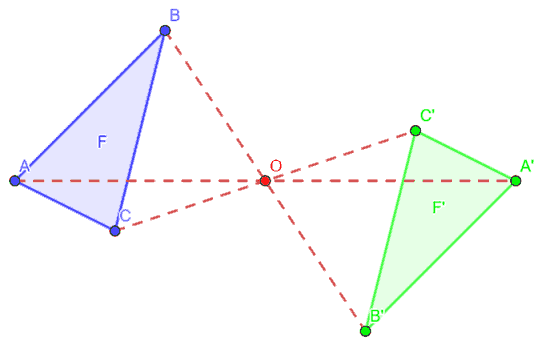
Possiamo notare che essa equivale ad una ROTAZIONE di 180° avente per centro il punto O.
Infatti, iniziamo ad effettuare la rotazione del punto A di centro O e di ampiezza 180°.
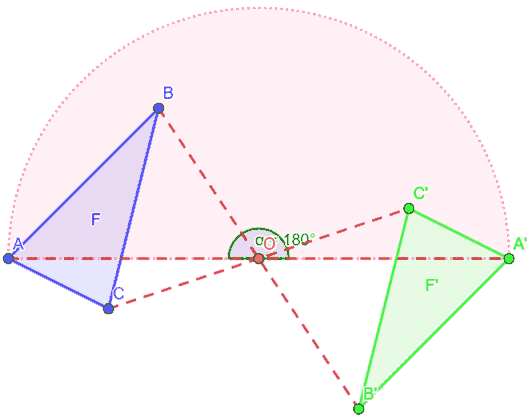
Come si può vedere si ottiene il punto A'.
Ora facciamo la stessa cosa con il punto B e noteremo che otteniamo il punto B'.
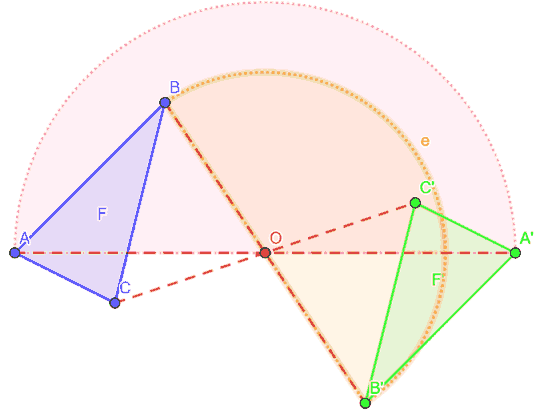
Ed infine con il punto C ed otterremo C'.
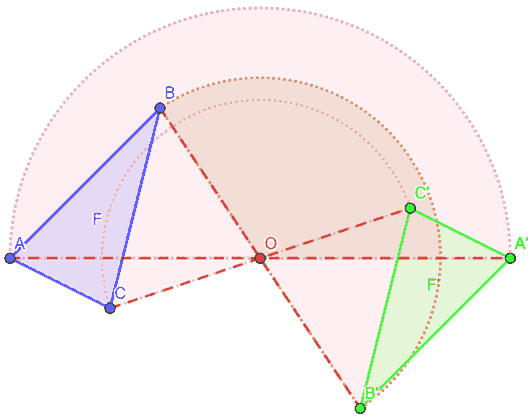
E' evidente, quindi, che la SIMMETRIA CENTRALE di centro O equivale ad una ROTAZIONE di 180° avente per centro il punto O.
Nella prossima lezione ci occuperemo del prodotto di due simmetrie centrali.






