SEMPLIFICAZIONE DEI RADICALI: CASI PARTICOLARI

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• Proprietà invariantiva dei radicali
• Semplificazione dei radicali
• Radicali con indice dispari
• L'insieme dei numeri reali

Nella lezione precedente abbiamo visto come possiamo procedere a SEMPLIFICARE un RADICALE.

Abbiamo visto che la regola è applicabile nel caso in cui il RADICANDO sia MAGGIORE o UGUALE a ZERO.

In questa lezione andremo ad esaminare alcuni CASI PARTICOLARI di semplificazione dei radicali.

Partiamo dal seguente caso:

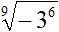
Qui il radicando è -3, quindi un numero negativo. Per cui, così come è scritto, il radicale non può essere semplificato.

Sappiamo, però, che un radicale di indice dispari con radicando negativo può essere scritto anche nel modo seguente:

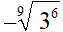
A questo punto, essendo il radicando positivo, possiamo applicare la nostra regola e, dato che sia 9 che 6 sono divisibili per 3, possiamo scrivere:

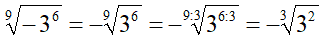
Supponiamo ora di avere:

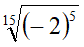
Anche in questo caso il radicando -2 è negativo. Ora

(-2)⁵ = -2⁵

infatti

-32 = -32

Quindi possiamo scrivere:

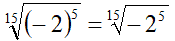
Siccome la radice ha indice dispari siamo tornati ad un caso del tutto simile a quello precedente. Quindi:

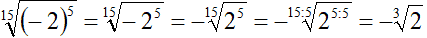
Veniamo ad un altro caso:

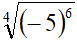
Qui, ad una prima lettura, il radicando potrebbe sembrare negativo (-5) ma così non è. Infatti:

(-5)⁶ = (+5)⁶

dato che

(-5)⁶ = + 15.625

(+5)⁶ = + 15.625.

Quindi possiamo scrivere:

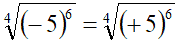
A questo punto, essendo il radicando positivo, possiamo procedere alla semplificazione:

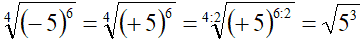
Mentre, se avessimo avuto

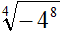
non avremmo potuto effettuare nessuna semplificazione poiché tale radice è priva di significato.

Infatti, l'indice della radice è pari e il radicando è negativo:

- 4⁸ = - 65.536.

Vediamo un ultimo caso:

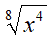
Osserviamo che in questo caso abbiamo:

• radicando una lettera;
• indice della radice PARI;
• esponente del radicando PARI.

Essendo l'esponente del radicando pari, il radicando è sempre positivo, quindi

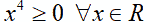
che si legge

x alla quarta maggiore o uguale a zero per qualsiasi x appartenente ai reali.

Ora si potranno avere due situazioni diverse:

• x è positivo o uguale a zero. In altre parole:

  x ≥ 0.

  
  
  

  In questo caso possiamo scrivere

  
  
  

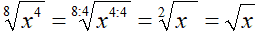
• x è negativo. In altre parole:

  x < 0.

  
  
  

  Poiché

  
  
  

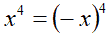
  in questo caso scriveremo:

  
  
  

  
  
  

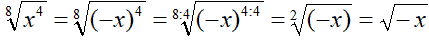
Quindi possiamo sintetizzare scrivendo che:

Lezione precedente - Lezione successiva

Indice degli argomenti sui radicali

Pubblicità/Advertising