DIVISIONE DI NUMERI RELATIVI
- I numeri relativi
- Rappresentazione grafica numeri relativi
- Operazioni con i numeri relativi
- Proprietà della divisione di numeri relativi
- La divisione
Si dice quoziente di due numeri relativi, presi in un dato ordine, di cui il secondo sia diverso da zero, un terzo numero che moltiplicato per il secondo dà per prodotto il primo.
Ad esempio, indichiamo con a, b, c tre numeri relativi.
Possiamo scrivere che
a : b = c
ponendo come condizione che
b sia
diverso da zero (si scrive 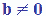 )
)
tale che
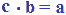 .
.
a, b
NUMERI RELATIVI
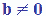
b diverso da zero
a : b = c
se 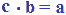
Il quoziente di due numeri relativi è il numero relativo che ha per valore assoluto il quoziente dei valori assoluti e per segno, il segno + se i due numeri hanno lo stesso segno (cioè se sono concordi), il segno - se i due numeri hanno segno contrario (cioè se sono discordi).
QUOZIENTE
DI DUE NUMERI RELATIVI
VALORE
ASSOLUTO: QUOZIENTE
DEI VALORI ASSOLUTI
SEGNO:
+ SE I
DUE NUMERI SONO CONCORDI
- SE I DUE NUMERI SONO DISCORDI
Esempi:
14 : (+2)
QUOZIENTE DI DUE NUMERI RELATIVI
VALORE
ASSOLUTO: QUOZIENTE
DEI VALORI ASSOLUTI
14 : 2 = 7
SEGNO
+ SE I
DUE NUMERI SONO CONCORDI
- SE I DUE NUMERI SONO DISCORDI
+ 14 e +2 CONCORDI: SEGNO
+
14 : (+2)
= + 7
-15 : (-3)
QUOZIENTE DI DUE NUMERI RELATIVI
VALORE
ASSOLUTO: QUOZIENTE
DEI VALORI ASSOLUTI
15 : 3 = 5
SEGNO
+ SE I
DUE NUMERI SONO CONCORDI
- SE I DUE NUMERI SONO DISCORDI
-15 e -3 CONCORDI: SEGNO
+
-15: (-3)
= + 5
-20 : (+2)
QUOZIENTE DI DUE NUMERI RELATIVI
VALORE
ASSOLUTO: QUOZIENTE
DEI VALORI ASSOLUTI
20 : 2 = 10
SEGNO
+ SE I
DUE NUMERI SONO CONCORDI
- SE I DUE NUMERI SONO DISCORDI
-20 e +2 DISCORDI: SEGNO
-
-20 : (+2)
= - 10
16 : (-8)
QUOZIENTE DI DUE NUMERI RELATIVI
VALORE
ASSOLUTO: QUOZIENTE
DEI VALORI ASSOLUTI
16 : 8 = 2
SEGNO
+ SE I
DUE NUMERI SONO CONCORDI
- SE I DUE NUMERI SONO DISCORDI
+16 e -8 DISCORDI: SEGNO
-
16 : (-8)
= - 2
Dividendo un numero relativo per (+1) si ottiene il numero relativo stesso.
Esempio:
+3 : (+1) = +3.
Dividendo un numero relativo per (-1) si ottiene l'opposto del numero relativo.
Esempio:
+3 :
(-1)
= -3.
Abbiamo detto che si definisce quoziente di due numeri relativi, presi in un dato ordine, un terzo numero che moltiplicato per il secondo dà per prodotto il primo e abbiamo posto come condizione che il secondo numero sia diverso da zero.
Proviamo ad immaginare di voler eseguire la seguente divisione:
-3 : 0.
Dovremmo trovare un numero relativo che, moltiplicato per zero, dia -3. Ma come sappiamo il prodotto di un numero relativo per zero è sempre uguale a zero (si veda a tale proposito la lezione sulla moltiplicazione di numeri relativi). Quindi non esiste un numero che moltiplicato per zero dia -3.
Se, invece, dobbiamo dividere lo zero per un numero relativo il risultato sarà sempre zero poiché l'unico numero che moltiplicato per un numero diverso da zero dà zero è lo zero.
Esempi:
0 : (+5) = 0
0 : (-6) = 0
0 : (+2) = 0.
- Esercizio 35 - Divisione di numeri relativi
- Esercizio 36 - Divisione di numeri relativi
- Esercizio 37 - Divisione di numeri relativi






