SISTEMI DI EQUAZIONI EQUIVALENTI
DUE SISTEMI di EQUAZIONI LINEARI si dicono EQUIVALENTI se ammettono le STESSE SOLUZIONI.
Se prendiamo un SISTEMA di EQUAZIONI LINEARI è possibile applicare su di esso alcune TRASFORMAZIONI che ci permettono di ottenere un SISTEMA EQUIVALENTE a quello dato.
Le TRASFORMAZIONI che applicate ad un sistema di equazioni lineari conducono ad un sistema equivalente sono:
- SCAMBIARE due equazioni tra loro;
- MOLTIPLICARE i DUE MEMBRI di un'equazione per un NUMERO DIVERSO da ZERO;
- SOMMARE a membro a membro, ad un'equazione un'altra equazione i cui due membri sono stati MOLTIPLICATI per un numero diverso da zero.
Esempio.
Consideriamo il seguente sistema
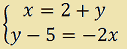
Ora scambiamo tra loro le due equazioni. Avremo:
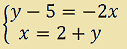
Otteniamo un sistema equivalente a quello dato, cioè che ammette le stesse soluzioni.
Ora, partendo sempre dal primo sistema di equazioni scritto, moltiplichiamo i due membri di un'equazione, ad esempio la seconda, per il numero 3. Avremo:
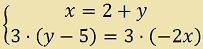
Anche questo sistema è equivalente a quello dato.
Infine, partendo sempre dal primo sistema scritto, sommiamo a membro a membro alla seconda equazione la prima moltiplicata per 2. Avremo
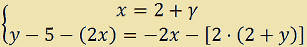
E anche questo è un sistema equivalente a quello dato.






