RIDUZIONE A FORMA CANONICA DI UNA MATRICE
Nella lezione precedente abbiamo visto come, partendo da una matrice A, è possibile ridurre tale matrice a FORMA CANONICA.
Nell'esempio da noi considerato abbiamo ipotizzato che
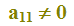
e
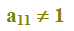
Ora vediamo cosa accade in queste due ipotesi.
PRIMO CASO:
a11 = 0.
In questo caso la prima trasformazione da effettuare consiste in uno SPOSTAMENTO per RIGHE o per COLONNE in modo da trasferire in quella posizione un ELEMENTO DIVERSO da ZERO.
A questo punto si può procedere come nell'esempio visto nella lezione precedente.
SECONDO CASO:
a11 = 1.
In questo caso il primo elemento della matrice è già uguale ad uno. Inizieremo, allora, con l'ANNULLARE gli altri ELEMENTI della PRIMA COLONNA.






