COMPLEMENTO ALGEBRICO
- Matrice
- Matrice quadrata
- Determinante di una matrice quadrata
- Calcolo del determinante di una matrice di ordine 2
- Minore complementare
Consideriamo una matrice quadrata A ed un suo elemento aij.
Si chiama COMPLEMENTO ALGEBRICO dell'elemento aij il PRODOTTO del suo MINORE COMPLEMENTARE per (-1)i+j.
Ovvero
COMPLEMENTO ALGEBRICO di aij
=
(-1)i+j· Mij
Esempio.
Consideriamo la matrice quadrata A:
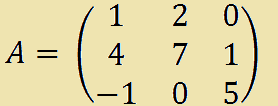
Ora prendiamo l'elemento a12 ovvero l'elemento che occupa la prima riga e la seconda colonna. Esso è l'elemento 2. Calcoliamo il minore complementare:
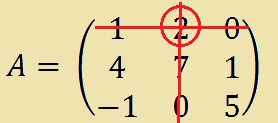
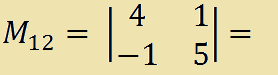
= [4 x 5] - [1 x (-1)] =
= 20 - (-1) =
= 20 + 1 = 21.
Il COMPLEMENTO ALGEBRICO di a12 è dato da:
(-1)1+2 ·M12 =
= (-1)3 · 21=
= -1· 21 = -21.
Quindi -21 è il complemento algebrico di a12.
Vediamo un altro esempio partendo sempre dalla matrice quadrata A:
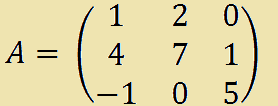
Ora prendiamo l'elemento a31 ovvero l'elemento che occupa la terza riga e la prima colonna. Esso è l'elemento -1 e calcoliamo il minore complementare:
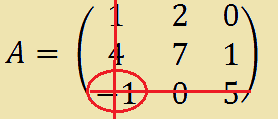
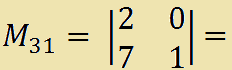
= [2 x 1] - [0 x 7] =
= 2 - 0 = 2.
Quindi 2 è il minore complementare di a31.
Il COMPLEMENTO ALGEBRICO di a31 è dato da:
(-1)3+1 ·M12 =
= (-1)4 ·2 =
= 1· 2 = 2.
Quindi -2 è il complemento algebrico di a31.






