CALCOLO DEL DETERMINANTE DI UNA MATRICE DI ORDINE 2
- Matrice
- Matrice quadrata
- Determinante di una matrice quadrata
- Calcolo del determinante di una matrice
- Calcolo del determinante di una matrice di ordine 1
Continuiamo ad esaminare i diversi metodi di CALCOLO del DETERMINANTE di una matrice quadrata.
Se abbiamo una MATRICE di ORDINE 2, il suo DETERMINANTE è dato dal PRODOTTO degli ELEMENTI della DIAGONALE PRINCIPALE DIMINUITO del PRODOTTO degli ALTRI DUE ELEMENTI.
In altre parole, se dobbiamo calcolare il DETERMINANTE di una MATRICE di ORDINE 2:
- eseguiamo il PRODOTTO degli ELEMENTI presenti sulla DIAGONALE PRINCIPALE;
- eseguiamo il PRODOTTO degli ALTRI due ELEMENTI;
- SOTTRAIAMO al PRIMO PRODOTTO ottenuto il SECONDO.
Esempio.
Supponiamo di avere la matrice
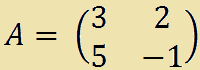
Ora vediamo come si calcola il suo determinante. Nell'immagine successiva abbiamo indicato con il colore rosso gli elementi della diagonale principale e con il colore azzurro gli altri elementi:
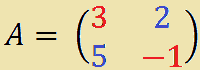
Ora procediamo al calcolo del determinante di A:
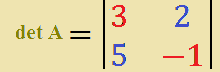
Ora:
- eseguiamo il prodotto degli
elementi della diagonale principale, ovvero eseguiamo il prodotto
di 3 e -1
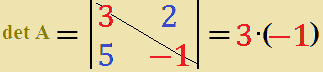
- e sottraiamo ad esso il prodotto
degli altri due elementi, ovvero sottraiamo il prodotto di 2
e 5
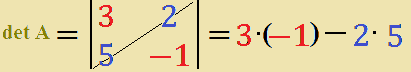
Quindi il nostro determinante sarà:
det
A = 3 ·
(-1) -
2 ·
5 =
-3 - 10 = -13.
Dunque il determinante
della nostra matrice quadrata di ordine due è -13.
Facciamo un altro esempio. Calcoliamo il determinante della matrice B:
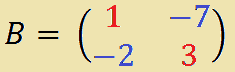
Abbiamo già indicato con il colore rosso gli elementi della diagonale principale e con il colore azzurro gli altri elementi.
Ora procediamo al calcolo del determinante:
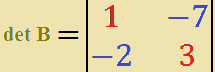
det B = 1 · 3 - (-7) · (-2) = 3 - (+14) =
=
3 - 14 = -11.
Il determinante di B è uguale a -11.






