SOTTOMATRICE PRINCIPALE DI TESTA
Nella lezione precedente abbiamo appreso che si chiama
SOTTOMATRICE PRINCIPALE di A una
- SOTTOMATRICE di A
- la cui DIAGONALE PRINCIPALE è costituita da ELEMENTI della DIAGONALE PRINCIPALE di A.
Ora, posto che A sia una matrice di ordine n, una SOTTOMATRICE PRINCIPALE di A costituita dalle PRIMEk RIGHE e dalle PRIME k COLONNE di A è detta SOTTOMATRICE PRINCIPALE di TESTA o SOTTOMATRICE PRINCIPALE di GUIDA della matrice A.
Esempio.
Consideriamo la matrice quadrata A di ordine 4.
Quindi avremo
n = 4.
La nostra matrice sarà:
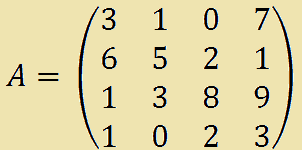
Ora scegliamo un valore di k tale che
k < n
che si legge
k minore di n.
Ad esempio poniamo
k
= 2.
Consideriamo la SOTTOMATRICE di A ottenuta prendendo dalla matrice A solamente le prime due righe e le prime due colonne. Avremo:
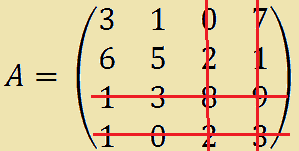
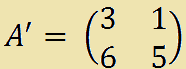
La matrice A' è una SOTTOMATRICE PRINCIPALE di A dato che gli elementi della sua diagonale principale sono anche elementi della diagonale principale di A.
Questa sottomatrice principale si dice SOTTOMATRICE PRINCIPALE di TESTA o SOTTOMATRICE PRINCIPALE di GUIDA.






