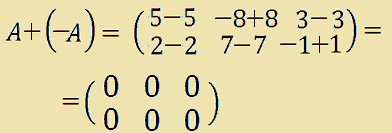MATRICE OPPOSTA
In una lezione precedente abbiamo appreso che il PRODOTTO SCALARE è il PRODOTTO di una MATRICE per uno SCALARE, ovvero per un numero reale.
Indichiamo con k uno scalare e con A la matrice.
Il PRODOTTO SCALARE si indica con
k · A.
Sappiamo, inoltre che il prodotto scalare è la MATRICE che si ottiene MOLTIPLICANDO ogni ELEMENTO di A per k.
Ora esaminiamo un caso particolare di prodotto scalare, ovvero il caso in cui
k = -1.
Vediamo un esempio. Supponiamo che la matrice A sia la seguente:
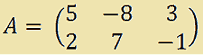
Avremo:

La matrice che abbiamo ottenuto si dice MATRICE OPPOSTA di A e si scrive anche -A.
Come si può notare dall'esempio precedente la MATRICE OPPOSTA di A si ottiene CAMBIANDO ORDINATAMENTE DI SEGNO i suoi elementi.
Facciamo un esempio. Sia B la seguente matrice:
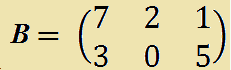
La matrice opposta di B sarà:
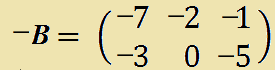
E' abbastanza evidente che data una matrice A di qualsiasi ordine essa sia, ESISTE SEMPRE LA MATRICE OPPOSTA -A.
Inoltre la SOMMA tra la matrice A e la MATRICE OPPOSTA -A, è una matrice i cui ELEMENTI SONO TUTTI UGUALI A ZERO e che vedremo meglio in seguito, prende il nome di MATRICE NULLA.
Infatti:
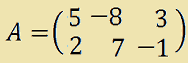
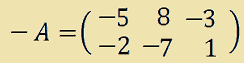
Avremo: