PRODOTTO TRA VETTORI
In una precedente lezione abbiamo visto che, una MATRICE, prende il nome di:
- VETTORE RIGA se è formata da UNA SOLA RIGA e da n colonne. Quindi si tratterà di una matrice di ordine (1 x n);
- VETTORE COLONNA se è formata da UNA SOLA COLONNA e da m righe. Quindi si tratterà di una matrice di ordine (m x 1).
Supponiamo di avere:
- un VETTORE RIGA formato da n colonne, che chiameremo A e che quindi ha ordine (1 x n);
- un VETTORE COLONNA formato da n righe, che chiameremo B e che quindi ha ordine (n x 1).
Il PRODOTTO di A per B viene detto PRODOTTO di un VETTORE RIGA PER un VETTORE COLONNA o PRODOTTO TRA VETTORI. A volte si parla anche di PRODOTTO INTERNO o PRODOTTO RIGHE PER COLONNE.
Tale prodotto è un NUMERO che si ottiene SOMMANDO i PRODOTTI degli ELEMENTI della RIGA di A per gli ELEMENTI della COLONNA di B.
Ovvero:
A · B = a11 · b11 + a12 · b21 +.... + a1n · bn1.
Vediamo come procedere con un esempio.
Siano
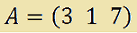
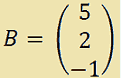
La matrice A è di ordine (1 x 3). Mentre la matrice B è di ordine (3 x 1).
Poiché il numero delle colonne della prima matrice è uguale al numero delle righe della seconda matrice è possibile eseguire il prodotto tra le due matrici. Il risultato si ottiene sommando:
- il prodotto dell'elemento che occupa la prima riga e la prima colonna nella matrice A (3) con l'elemento che occupa la prima riga e la prima colonna nella matrice B (5);
- il prodotto dell'elemento che occupa la prima riga e la seconda colonna nella matrice A (1)con l'elemento che occupa la seconda riga e la prima colonna nella matrice B (2);
- il prodotto dell'elemento che occupa la prima riga e la terza colonna nella matrice A (7) con l'elemento che occupa la terza riga e la prima colonna nella matrice B (-1).
In altre parole:

Quindi avremo:

Vediamo un altro esempio:



A · B = 2 · (-1) + 0 · 8 + (-3) ·4 =
= -2 +0 -12 = -14.
Nella prossima lezione vedremo le proprietà di cui gode il prodotto righe per colonne.






