PROPRIETA' DEL PRODOTTO DI UNA MATRICE PER UNO SCALARE
Nella lezione precedente abbiamo parlato del PRODOTTO di una MATRICE per uno SCALARE detto anche PRODOTTO SCALARE.
Ora vediamo di quali PROPRIETA' gode il PRODOTTO SCALARE.
Indichiamo con k e h due numeri reali e con A e B due matrici.
Il PRODOTTO SCALARE gode delle seguenti PROPRIETA':
- (k+h)
· A = k·A + h·A
Esempio:
k = 3
h = 5

Eseguiamo

Eseguiamo la somma di 3 + 5 e poi moltiplichiamo il risultato ottenuto, ovvero 8, per A:
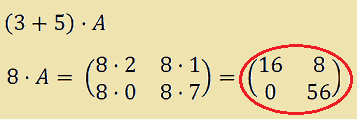
Ora, invece, eseguiamo il prodotto di 3 per A e di 5 per A e sommiamo le due matrici ottenute. Avremo:

Come possiamo notare, la matrice ottenuta nei due casi, è la stessa:
- k·
(A+B) = k·A + k·B
Esempio:
k = 3


Eseguiamo prima la somma di A+B.

Ora moltiplichiamo la matrice somma appena ottenuta per 3:

Ora, invece, moltiplichiamo 3 per A e 3 per B e successivamente sommiamo tra loro le due matrici ottenute:

Come possiamo notare, la matrice ottenuta con i due diversi procedimenti è la stessa.
- (k·h)·
A = k· (h·A)
Esempio:
k = 3
h = 2

Moltiplichiamo 3 per 2 e poi moltiplichiamo il prodotto ottenuto per A:
(3·2) = 6

Ora, invece, moltiplichiamo 2 per A e successivamente, moltiplichiamo il prodotto ottenuto per 3:

Anche in questo caso il risultato è analogo al precedente.
- 1·
A = A
Esempio:

Avremo:

Notiamo che il prodotto è esattamente uguale alla matrice A.






