INSIEME DELLE PARTI
- Nozione di insieme
- Insiemi finiti e infiniti
- Cardinalità di un insieme finito
- Insieme vuoto
- Sottoinsiemi di un insieme
- Sottoinsiemi propri e impropri
- Casi particolari dell'elevazione a potenza
Supponiamo di avere il seguente INSIEME:
A = {2, 4, 6}.
Vediamo ora quali sono i suoi possibili SOTTOINSIEMI:
{2}
{4}
{6}
{2, 4}
{2, 6}
{4, 6}.
Parlando di SOTTOINSIEMI PROPRI ed IMPROPRI abbiamo appreso che dato un insieme A esso ammette sempre DUE SOTTOINSIEMI:
- A STESSO;
- l'INSIEME VUOTO { }.
Quindi, aggiungendo anche A e l'insieme vuoto, tutti i sottoinsiemi del nostro insieme A saranno:
{}
{2}
{4}
{6}
{2, 4}
{2, 6}
{4, 6}
{2, 4, 6}.
Ora scriviamo l'insieme formato da questi sottoinsiemi. Per rendere più chiara la cosa abbiamo scritto in verde i sottoinsiemi dell'insieme A e in blu l'insieme formato da tali sottoinsiemi. Avremo:
{ {}, {2}, {4}, {6}, {2, 4}, {2, 6}, {4, 6}, {2, 4, 6} }.
L'insieme che abbiamo appena scritto si dice INSIEME DELLE PARTI DI A.
Quindi, l'INSIEME DELLE PARTI DI A è l'insieme i cui ELEMENTI sono tutti i SOTTOINSIEMI di A, compreso l'INSIEME VUOTO e A STESSO.
L' INSIEME DELLE PARTI DI A viene indicato con il simbolo
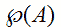
oppure
2A
che si legge
insieme delle parti di A
oppure
insieme potenza di A
o ancora
booleano di A.
L'INSIEME DELLE PARTI DI A sarà FINITO o INFINITO a seconda che A sia un INSIEME FINITO o un INSIEME INFINITO.
Indichiamo con n il numero degli elementi di cui è formato l'insieme A. n rappresenta la CARDINALITA' di A e si scrive
Car(A) = n.
Supponiamo che A sia l'INSIEME VUOTO. Cioè n = 0. Avremo:
A = { }.
Gli unici SOTTOINSIEMI di A sono
- l'insieme vuoto - { }
- A stesso, cioè { }.
poiché l'insieme vuoto è uguale ad A,
l'unico SOTTOINSIEME di A è
{ }.
Quindi l'INSIEME DELLE PARTI DI A sarà
{ {} }.
Quindi
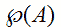 è
formato da un solo elemento.
è
formato da un solo elemento.
Allora possiamo dire che la CARDINALITA' dell'INSIEME DELLE PARTI di A è 1.
Immaginiamo ora che A sia un insieme formato da un SOLO ELEMENTO, cioè n = 1. Ovvero:
A = {a}.
I SOTTOINSIEMI di A sono
{ } - insieme vuoto
{a}
{a} - A stesso.
poiché {a} = {a},
l'INSIEME DELLE PARTI DI A sarà
{ {}, {a} }.
Quindi
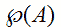 è
formato da due elementi.
è
formato da due elementi.
Allora possiamo dire che la CARDINALITA' dell'INSIEME DELLE PARTI di A è 2.
Supponiamo ora che A sia un insieme formato da un DUE ELEMENTI, cioè n = 2. Ovvero:
A = {a, b}.
I SOTTOINSIEMI di A sono
{ }
{a}
{b}
{a, b}.
L'INSIEME DELLE PARTI DI A sarà
{ {}, {a}, {b}, {a, b} }.
Quindi
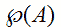 è
formato da quattro elementi.
è
formato da quattro elementi.
Allora possiamo dire che la CARDINALITA' dell'INSIEME DELLE PARTI di A è 4.
Abbiamo visto in precedenza che, se A è formato da 3 elementi, l'insieme delle parti di A è formato da 8 elementi.
Ricapitoliamo quanto abbiamo detto:
| n ELEMENTI DI A | n ELEMENTI DELL'INSIEME DELLE PARTI DI A |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
Generalizzando possiamo dire che, se l'insieme A ha un numero FINITO di ELEMENTI n, l'INSIEME DELLE PARTI di A è pure esso FINITO e avrà un numero di elementi pari a 2n.
Infatti:
| n ELEMENTI DI A | n ELEMENTI DELL'INSIEME DELLE PARTI DI A | 2n |
|---|---|---|
| 0 | 1 | 20 = 1 |
| 1 | 2 | 21 = 2 |
| 2 | 4 | 22 = 4 |
| 3 | 8 | 23 = 8 |






