LA SEMIRETTA
Prendiamo una RETTA a

Su di essa disegniamo un punto Q:
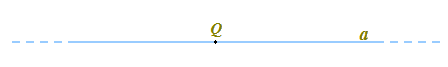
Notiamo che la retta viene divisa dal punto Q in due parti. Chiameremo queste due parti, rispettivamente a1 e a2:
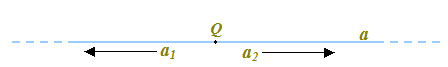
Notiamo che a1 e a2:
- iniziamo entrambe dal punto Q;
- si trovano da parti opposte rispetto a Q;
- ognuna di esse è infinita dalla parte opposta a Q.
Le due parti della retta a1 e a2 prendono il nome di SEMIRETTE.
Possiamo affermare, quindi, che una SEMIRETTA è ciascuna delle DUE PARTI in cui una RETTA rimane DIVISA da un PUNTO.
Notiamo che la SEMIRETTA ha un inizio (il punto Q), ma non ha una fine.
Essa ha una sola dimensione: la LUNGHEZZA.
Torniamo ad osservare la nostra immagine:
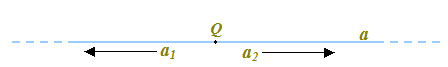
Il punto Q prende il nome di ORIGINE delle semirette a1 e a2.
Le due SEMIRETTE in cui rimane divisa una retta da un suo punto, si dicono SEMIRETTE OPPOSTE.
Quindi le semirette a1 e a2 nelle quali rimane divisa la retta a dal punto Q, sono due semirette opposte.
La SEMIRETTA può essere indicata in due modi diversi:
- con una lettera minuscola;
- con due LETTERE MAIUSCOLE di cui la prima è l'ORIGINE della semiretta e la seconda un QUALSIASI ALTRO PUNTO della semiretta.
Esempio:
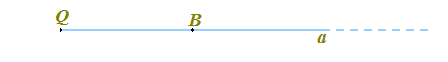
Abbiamo disegnato una semiretta avente come origine il punto Q.
Su questa semiretta abbiamo disegnato un altro punto qualsiasi B.
Ora possiamo indicare la nostra semiretta:
- con una lettera minuscola, nel nostro caso abbiamo scelto a;
- oppure con le lettere maiuscole QB.
Vediamo un altro esempio:

Anche in questo caso abbiamo disegnato una semiretta avente come origine il punto Q.
Su questa semiretta abbiamo disegnato un altro punto qualsiasi C.
Ora possiamo indicare la nostra semiretta:
- con una lettera minuscola, nel nostro caso abbiamo scelto b;
- oppure con le lettere maiuscole QC.
ATTENZIONE!!! Se indichiamo la semiretta con due LETTERE MAIUSCOLE dobbiamo indicare per prima sempre l'origine e poi un altro punto.






