ARCOSENO
Nella lezione precedente abbiamo richiamato il concetto di funzione inversa e abbiamo detto che le FUNZIONI GONIOMETRICHE sono INVERTIBILI solamente RESTRINGENDO il DOMINIO della funzione ad un intervallo di angoli in modo che la funzione goniometrica diventi biunivoca.
Fatta questa premessa, in questa lezione ci occuperemo dell'ARCOCOSENO.
Partiamo dalla funzione:
y = sen α
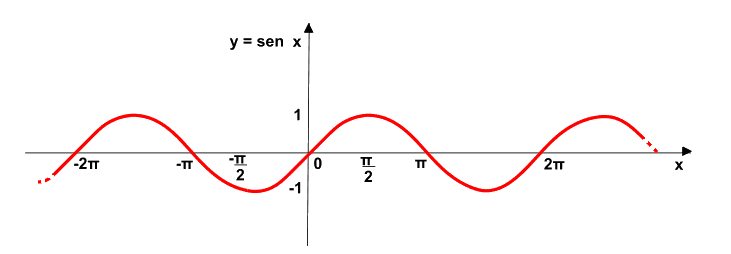
Come sappiamo il SENO dell'angolo α può assumere solamente valori compresi tra -1 e 1: questo è il suo CODOMINIO.
La funzione seno è definita per qualsiasi numero reale: l'insieme dei numeri reali R è il suo DOMINIO.
Queste caratteristiche emergono chiaramente dal grafico della funzione seno:
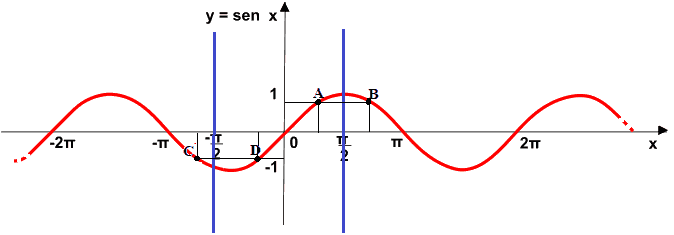
Affinché la funzione seno sia invertibile è necessario limitare il suo dominio in modo da rendere la funzione biunivoca: andremo, quindi, a considerare l'intervallo -π/2, π/2, cioè:
[-π/2, π/2]
Infatti, andando oltre questo intervallo (sia a destra che a sinistra) accade che ad uno stesso valore di y sono associati due valori di x come possiamo vedere, ad esempio, con i punti A e B e con i punti C e D.
La FUNZIONE INVERSA del SENO si chiama ARCOSENO e si indica con i simboli:
arcsen
oppure
arcsin
o ancora
asin
che si leggono tutti
arcoseno.
Può essere indicato, però, anche nel modo seguente:
sen-1
oppure
sin-1
che si leggono entrambi
seno alla meno 1.
Supponiamo di avere un angolo, che chiamiamo y il cui seno vale x, ovvero:
x = sen y
La funzione inversa sarà:
y = arcsen x
In altre parole l'ARCOSENO è l'ANGOLO che ha un determinato valore di seno.
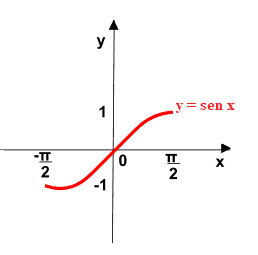
Vediamo, adesso, come possiamo costruire il GRAFICO della FUNZIONE ARCOSENO.
Iniziamo col prendere il GRAFICO della FUNZIONE SENO nell'intervallo [-π/2 , π/2]:
Ora disegniamo la BISETTRICE del PRIMO e del TERZO quadrante, ovvero la retta di equazione
y = x
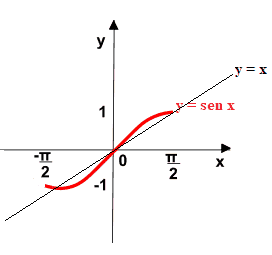
Ora disegniamo la curva SIMMETRICA a y = sen x rispetto alla bisettrice del primo e terzo quadrante:
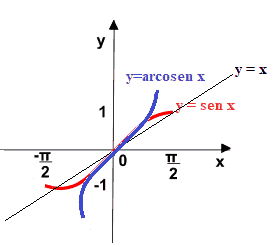
Quello che abbiamo ottenuto è il GRAFICO della FUNZIONE ARCOSENO che riportiamo nell'immagine sottostante dove viene evidenziato come la funzione arcocoseno sia stata ottenuta dalla funzione seno scambiando i valori della x con quelli della y.
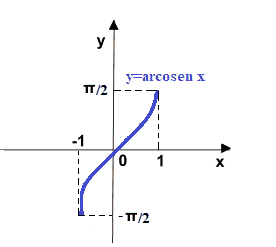
E' evidente, quindi, che la FUNZIONE ARCOSENO ha come
DOMINIO: [ -1 , +1 ]
che si legge
intervallo chiuso -1, +1
CODOMINIO: [ -π/2 , +π/2 ]
che si legge
intervallo chiuso -pi greco mezzi, +pi greco mezzi






