VARIAZIONI DELLE FUNZIONI SENO E COSENO
Supponiamo che un punto P percorra tutta la circonferenza goniometrica partendo dal punto A in verso antiorario:
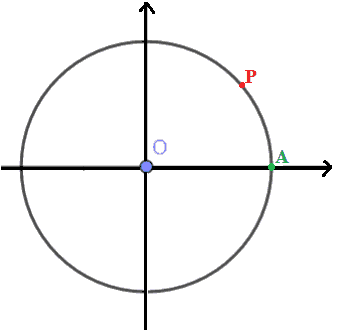
Ricordiamo che:
- il SENO dell'angolo α è uguale all'ORDINATA del punto P;
- il COSENO dell'angolo α è uguale all'ASCISSA del punto P;
- e che il RAGGIO della circonferenza goniometrica è uguale ad 1.
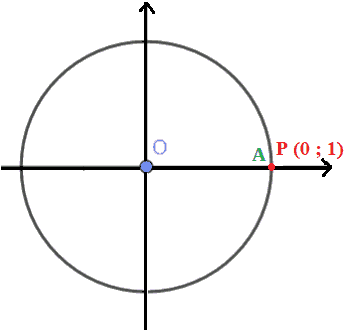
Quando il punto P si trova nel punto A il coseno dell'angolo α è pari ad 1, mentre il seno è pari a 0.
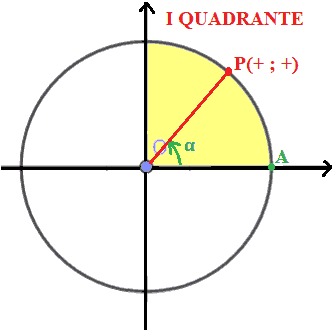
Quando il punto P percorre il tratto della circonferenza goniometrica compreso nel I QUADRANTE sia il coseno che il seno assumono sempre valori POSITIVI.
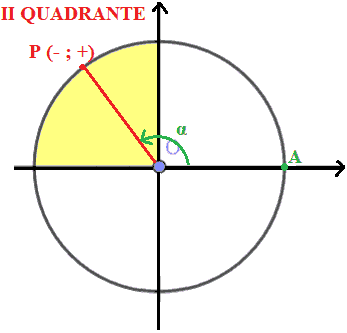
Quando il punto P raggiunge il punto B il coseno dell'angolo α è pari a 0, mentre il seno è pari ad 1.

Quando il punto P percorre il tratto della circonferenza goniometrica compreso nel II QUADRANTE il COSENO assume valori NEGATIVI mentre il SENO assume valori POSITIVI.
Quando il punto P raggiunge il punto C il coseno dell'angolo α è pari ad -1, mentre il seno è pari a 0.
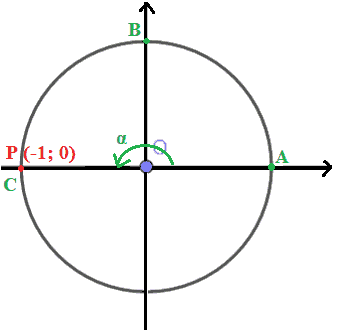
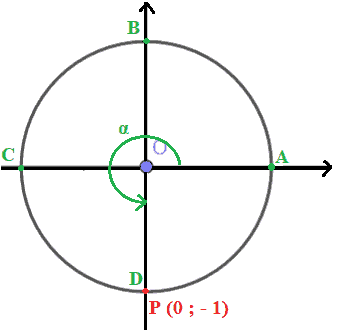
Quando il punto P percorre il tratto della circonferenza goniometrica compreso nel III QUADRANTE sia il coseno che il seno assumono valori NEGATIVI.
Quando il punto P raggiunge il punto D il coseno dell'angolo α è pari a 0, mentre il seno è pari ad -1.
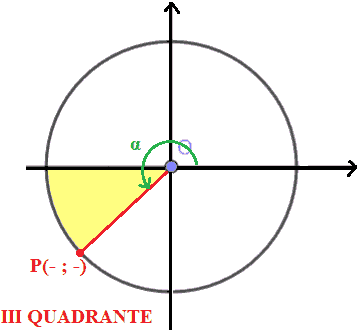
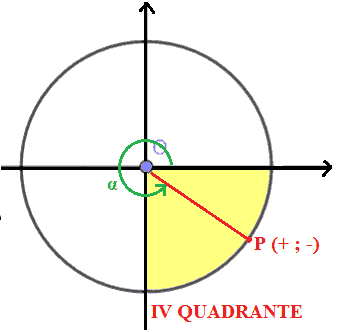
Quando il punto P percorre il tratto della circonferenza goniometrica compreso nel IV QUADRANTE il COSENO assume valori POSITIVI mentre il SENO assume valori NEGATIVI.
Notiamo, quindi, che qualsiasi sia la posizione del punto P sulla circonferenza goniometrica, la sua ascissa e la sua ordinata assumono sempre valori compresi tra -1 e 1. Quindi possiamo scrivere:
-1 ≤ cos α ≤ 1
-1 ≤ sen α ≤ 1
Pertanto possiamo dire che il CODOMINIO della funzione seno e della funzione coseno è dato da
[-1 , +1]
che si legge
intervallo chiuso meno 1, più 1






