ANGOLI DEL PARALLELOGRAMMA
- Parallelogramma
- Parallelogramma: definizioni
- Proprietà del parallelogramma
- Diagonali del parallelogramma
- Diagonali del parallelogramma
- Lati del parallelogramma
- Angoli adiacenti del parallelogramma
- Diagonale di un poligono
- Triangoli
- Figure geometriche equivalenti e figure geometriche congruenti
In una delle lezioni precedenti abbiamo visto che che ogni PARALLELOGRAMMA è DIVISO da ciascuna DIAGONALE in DUE TRIANGOLI CONGRUENTI:
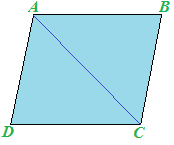
Essendo i triangoli ABC
e ACD congruenti anche gli
angoli  e
e  sono
congruenti:
sono
congruenti:

Ora osserviamo che la diagonale AC divide ognuno dei due angoli restanti in due parti che abbiamo chiamato rispettivamente A' (che si legge A primo) e A'' (che si legge A secondo) e C' (che si legge C primo) e C'' (che si legge C secondo):

Ora notiamo che :
- l'angolo A è la somma degli angoli A' e A'';
- l'angolo C è la somma degli angoli C' e C''.
Poiché gli angoli A' e C' sono congruenti e lo sono anche gli angoli A'' e C'', gli angoli A e C sono anch'essi congruenti dato che essi non sono altro che la somma di angoli congruenti.
Quindi possiamo affermare che in ogni PARALLELOGRAMMA gli ANGOLI OPPOSTI sono CONGRUENTI.






