NOTAZIONE SCIENTIFICA DI UN NUMERO
A volte può capitare di trovarci di fronte a grandezze espresse da NUMERI MOLTO GRANDI o MOLTO PICCOLI.
Ad esempio:
- la distanza tra la Terra e il Sole è di 150.000.000 km;
- il raggio terrestre misura all'incirca 700.000.000 m;
- il diametro di un globulo rosso è pari a 0,007 mm.
Come possiamo notare, in questi casi, ci troviamo di fronte a numeri molto grandi (nei primi due casi) o molto piccoli (nell'ultimo caso).
Questi numeri possono essere scritti anche sotto forma del PRODOTTO di DUE FATTORI di cui uno è una POTENZA DEL 10.
Cioè, possiamo scrivere, il generico numero n come prodotto tra k e la potenza ennesima di 10. Ovvero:
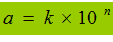
Questa che vedete sopra si chiama NOTAZIONE SCIENTIFICA.

Occorre tenere presente che k deve essere un numero compreso tra 1 e 10 o, tutt'al più, uguale a 1.
Quindi:
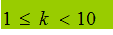
Inoltre n è sempre un numero intero.
Quindi, n è un NUMERO INTERO, ma può essere sia UN NUMERO POSITIVO che un NUMERO NEGATIVO.
Osservate questi tre esempi:
3 x 102
3 x 10-3
0,3 x 102.
I primi due numeri sono scritti in NOTAZIONE SCIENTIFICA. Il terzo no. Perché?
Vi ricordate che k deve avere un valore maggiore di 1 e minore di 10: nei primi due casi ciò si verifica, mentre nel terzo caso abbiamo un valore inferiore a 1 (0,3). In quest'ultimo caso si parla di NOTAZIONE ESPONENZIALE.
Quindi:
3 x 102 NOTAZIONE SCIENTIFICA
3 x 10-3 NOTAZIONE SCIENTIFICA
0,3 x 102 NOTAZIONE ESPONENZIALE.
Torniamo alla NOTAZIONE SCIENTIFICA e vediamo come è possibile scrivere un numero, che chiameremo a, in notazione scientifica, ricordando che:
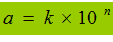
-
per prima cosa occorre contare il NUMERO
DI POSTI DI CUI OCCORRE SPOSTARE LA VIRGOLA in modo da
ottenere un numero k MAGGIORE O UGUALE AD 1
e MINORE DI 10. Questo numero
rappresenta la nostra n;
Esempio:
prendiamo il numero 150.000.000
esso ha 7 zeri. Però se mettiamo n = 7 avremo k = 15 cioè un numero maggiore di 10.
Allora poniamo n = 8, cioè spostiamo la virgola di 8 posti verso sinistra, e k = 1,5, cioè un numero compreso tra 1 e 10.
Per cui avremo:
a = 1,5 x 108.
- poi occorre applicare la seguente regola:
se a è MAGGIORE o UGUALE ad UNO, esso verrà scritto in notazione scientifica con n POSITIVO;
se a è COMPRESO TRA ZERO e UNO, esso verrà scritto in notazione scientifica con n NEGATIVO.
Esempio:
prendiamo il numero 150.000.000.
Quindi
a =150.000.000
si tratta di un numero maggiore di 1.
Pertanto n sarà positivo.
Quindi
150.000.000 = 1,5 x 108.
Ora vediamo cosa accade se prendiamo il numero 0,0000005.
Quindi
a = 0,0000005
si tratta di un numero compreso tra 0 e 1.
Pertanto n sarà negativo.
Quindi
0,0000005 = 5 x 10-7 .
Infatti:
0,0000005 = 5 x 1/10.000.000 = 5 x 1/107 = 5 x 10-7.
Vediamo insieme qualche altro esempio.
NUMERO: 23.000.000.000
VALORE di n: 10
(numero di posti di cui spostare la virgola in
modo da avere k maggiore o uguale a 1 e minore di 10)
SEGNO DI n: a
maggiore di 1
segno di n +
NOTAZIONE SCIENTIFICA: 2,3 x
1010
NUMERO: 7.000.000.000
VALORE di n: 9
(numero di posti di cui spostare la virgola in
modo da avere k maggiore o uguale a 1 e minore di 10)
SEGNO DI n: a
maggiore di 1
segno di n +
NOTAZIONE SCIENTIFICA: 7 x 109
NUMERO: 0,000003
VALORE di n: 6
(numero di posti di cui spostare la virgola in
modo da avere k maggiore o uguale a 1 e minore di 10)
SEGNO DI n: a
minore di 1
segno di n -
NOTAZIONE SCIENTIFICA: 3 x 10-6
NUMERO: 0,00000015
VALORE di n: 7
(numero di posti di cui spostare la virgola in
modo da avere k maggiore o uguale a 1 e minore di 10)
SEGNO DI n: a
maggiore di 1
segno di n -
NOTAZIONE SCIENTIFICA: 1,5 x
10-7
- Ordine di grandezza di un numero
- Notazione scientifica e ordine di grandezza di un numero
- Operazioni con i numeri in notazione scientifica






