SOMMA DEGLI ANGOLI INTERNI DI UN POLIGONO

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• I poligoni
• Caratteristiche dei poligoni
• Angoli interni e angoli esterni di un poligono
• Angoli complementari, angoli supplementari, angoli esplementari

Disegniamo un poligono:

Ora disegniamo gli ANGOLI INTERNI e gli ANGOLI ESTERNI del poligono:

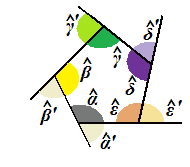
Abbiamo indicato gli angoli interni del poligono con le lettere dell'alfabeto greco:

α   β   γ   δ   ε

che si leggono

α Alfa

β Beta

γ Gramma

δ Delta

ε Epsilon.

 

Mentre gli angoli esterni li abbiamo indicati con:

α'   β'   γ'   δ'   ε'

che si leggono

α' Alfa primo

β' Beta primo

γ' Gramma primo

δ' Delta primo

ε' Epsilon primo.

Noi sappiamo che OGNI ANGOLO ESTERNO è ADIACENTE, e quindi SUPPLEMENTARE, dell'ANGOLO INTERNO avente lo STESSO VERTICE.

E sappiamo anche che due angoli supplementari misura 180°.

Quindi possiamo dire che:

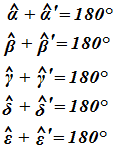
Quindi la SOMMA DEGLI ANGOLI INTERNI del nostro poligono e la SOMMA DEGLI ANGOLI ESTERNI è pari complessivamente a:

S_C = 5 x 180°

dove

S_C = somma complessiva delle ampiezze degli angoli interni ed esterni del poligono.

Sappiamo anche che in un POLIGONO qualsiasi, la SOMMA degli ANGOLI ESTERNI è pari a 360°.

Quindi possiamo scrivere:

S_E = 360°

dove

S_E = somma delle ampiezze degli angoli esterni del poligono.

Ora la SOMMA DEGLI ANGOLI INTERNI (S_I) è uguale alla SOMMA COMPLESSIVA DELLE AMPIEZZE DI ANGOLI INTERNI ED ESTERNI (S_C)meno la SOMMA DEGLI ANGOLI ESTERNI (S_E). Ovvero:

S_I = S_C - S_E

Ora noi sappiamo che

S_C = 5 x 180°

e che

S_E = 360°.

Quindi possiamo scrivere:

S_I = 5 x 180° - 360°.

Poichè:

360° = 2 x 180°.

Sostituendo il prodotto nella precedente uguaglianza avremo:

S_I = 5 x 180° - 2 x 180°.

Ma per la PROPRIETA' DISTRIBUTIVA DELLA MOLTIPLICAZIONE ciò equivale a scrivere:

S_I = (5 - 2) x 180°.

Quindi:

S_I = 3 x 180° = 540°.

L'esempio da noi fatto riguarda un poligono di 5 lati e 5 angoli.

Vediamo cosa accade con vari tipi di poligoni:

TRIANGOLO
3 lati e 3 angoli
S_C: 3 x 180°
S_E: 360° = 2 x 180°
S_I: 3 x 180° - 2 x 180° = (3 -2) x 180°

QUADRILATERO
4 lati e 4 angoli
S_C:4 x 180°
S_E: 360° = 2 x 180°
S_I: 4 x 180° - 2 x 180° = (4 -2) x 180°

PENTAGONO
5 lati e 5 angoli
S_C: 5 x 180°
S_E: 360° = 2 x 180°
S_I: 5 x 180° - 2 x 180° = (5 - 2 ) x 180°

ESAGONO
6 lati e 6 angoli
S_C: 6 x 180°
S_E: 360° = 2 x 180°
S_I: 6 x 180° - 2 x 180° = (6 -2) x 180°

Generalizzando, se indichiamo con n il numero di lati di un poligono (e dunque anche il numero di angoli) la SOMMA DEGLI ANGOLI INTERNI è pari a:

S_I = (n-2) x 180°.

Per approfondire questo argomento, leggi:

• Somma degli angoli esterni di un poligono

Indice degli argomenti sui poligoni

Pubblicità/Advertising