SOMMA DEGLI ANGOLI ESTERNI DI UN POLIGONO
Disegniamo il poligono ABCDE:
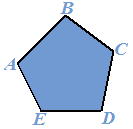
Ora disegniamo gli ANGOLI ESTERNI del poligono. Ricordiamo che sono angoli esterni del poligono, gli angoli formati da UN LATO del poligono e dal PROLUNGAMENTO di uno dei LATI CONSECUTIVI:

Abbiamo indicato gli angoli esterni del poligono con le lettere dell'alfabeto greco:
α β γ δ ε
che si leggono
α Alfa
β Beta
γ Gramma
δ Delta
ε Epsilon.
Ora prendiamo tutti gli ANGOLI ESTERNI del poligono e li riuniamo intorno ad un unico vertice in maniera che essi siano consecutivi a due a due:
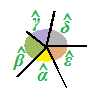
E' evidente che la SOMMA degli ANGOLI ESTERNI del POLIGONO è un ANGOLO GIRO, cioè misura 360#.
Possiamo ripetere l'esperimento con qualsiasi tipo di poligono ottenendo sempre il medesimo risultato:
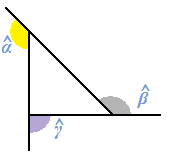

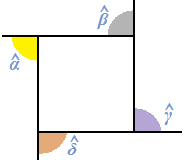
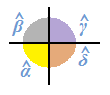
Quindi possiamo affermare che in un POLIGONO qualsiasi, la SOMMA degli ANGOLI ESTERNI è pari a 360°.






