L'INSIEME Q: SUA INADEGUATEZZA
- L'insieme dei numeri razionali relativi
- Operazioni con i numeri razionali
- L'insieme dei numeri naturali
- Radice quadrata
- Potenza di una frazione
Parlando dei NUMERI
RAZIONALI abbiamo detto che l'ESTRAZIONE
DI RADICE non
sempre è un'operazione interna in Q.
Consideriamo ad esempio la radice quadrata di 2:
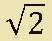
Non esiste nessun numero razionale che elevato al quadrato mi dia come risultato 2.
Quindi, se indichiamo con q un numero razionale, potremo dire che:
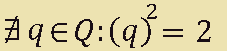
che si legge
non esiste un numero q appartenente all'insieme dei numeri razionali tale che q al quadrato è uguale a 2.
Ora dimostriamo, per assurdo, quanto abbiamo detto.
Essendo q un numero razionale possiamo scriverlo sotto forma di rapporto tra due numeri m ed n appartenenti ai naturali con n diverso da zero.
Quindi:
q = m/n
con
n ≠ 0.
Ora se esiste un numero q appartenente ai razionali, tale che il suo quadrato è uguale a 2 dovremmo poter scrivere:
q2 = (m/n)2 = 2.
Ma elevare una frazione al quadrato significa elevare al quadrato sia il numeratore che il denominatore. Quindi possiamo scrivere:
m2/n2 = 2.
Ora moltiplichiamo il primo e il secondo membro per n2 e avremo:
(m2/n2)· n2 = 2n2.
Semplifichiamo ed otteniamo:
m2 = 2n2.
Ora osserviamo i numeri naturali m ed n:
- se m
è un NUMERO
PARI esso contiene il fattore 2.
Di conseguenza m2
contiene il fattore 2
un numero pari di volte.
Esempio:
NUMERO PARI CONTIENE IL FATTORE 2 QUADRATO CONTIENE IL FATTORE 2 2 1 volta 4 2 volte 4 2 volte 16 4 volte 6 1 volta 36 2 volte 8 3 volte 64 6 volte 10 1 volta 100 2 volte - se m
è un NUMERO DISPARI
esso NON
contiene il fattore 2.
Di conseguenza anche m2
NON
contiene il fattore 2.
Esempio:
NUMERO DISPARI CONTIENE IL FATTORE 2 QUADRATO CONTIENE IL FATTORE 2 3 0 volte 9 0 volte 5 0 volte 25 0 volte 7 0 volte 49 0 volte 9 0 volte 81 0 volte 11 0 volte 121 0 volte - se n è un NUMERO PARI esso contiene il fattore 2. Di conseguenza n2 contiene il fattore 2 un numero pari di volte e 2n2 contiene il fattore 2 un numero dispari di volte;
- se n è un NUMERO DISPARI esso NON contiene il fattore 2. Di conseguenza n2 NON contiene il fattore 2 e 2n2 contiene il fattore 2 un numero dispari di volte.
Quindi, ricapitolando:
- m2 può contenere il fattore 2 o un numero pari di volte o può non contenerlo affatto;
- n2 contiene il fattore 2 sempre un numero dispari di volte.
Quindi, abbiamo dimostrato che non potrà mai essere vero che
m2 = 2n2.






