FUNZIONI REALI: IL SIGNIFICATO DI ALCUNI SIMBOLI
- Funzioni reali di variabile reale
- L'insieme dei numeri reali
- Sottoinsiemi di un insieme
- Sottoinsiemi propri e impropri
- Insieme vuoto
Nella lezione precedente abbiamo parlato di FUNZIONE REALE di UNA VARIABILE REALE per indicare una CORRISPONDENZA f che associa ad un numero reale UNO E UN SOLO numero reale.
Abbiamo indicato tale funzione con
y = f(x)
che si legge
y è uguale a f di x.
E abbiamo detto che questa funzione associa ad un NUMERO REALE x appartenente all'insieme X UNO E UN SOLO NUMERO REALE y appartenente all'insieme Y.
Indicheremo tale funzione così:
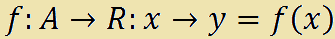
che si legge
f di A in R tale che associa x ad y è uguale ad f di x.
Poniamo, però, come condizione che:
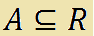
che si legge
A è sottoinsieme di R
Notiamo che abbiamo usato il simbolo di sottoinsieme improprio in quanto A può essere:
- sia un sottoinsieme proprio nel caso in cui ogni elemento di A appartiene ad R ma non viceversa;
- che un sottoinsieme improprio nel caso in cui ogni elemento di A appartiene ad R e viceversa e quindi l'insieme A coincide con l'insieme R.
Inoltre poniamo come condizione che:
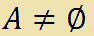
che si legge
A è diverso dall'insieme vuoto
Questa seconda condizione evita che A sia un insieme privo di elementi.
Quindi possiamo scrivere la nostra funzione anche nel modo seguente:
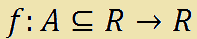
che si legge
f di A, contenuto o uguale ad R, in R.
Dove:
- A è un SOTTOINSIEME di R è può, eventualmente, coincidere con R;
- R è l'INSIEME dei NUMERI REALI;
- A è l'INSIEME DI DEFINIZIONE, cioè l'insieme dei valori di x a cui la funzione associa un valore di y, in altre parole il DOMINIO della funzione.






