TRASLAZIONE DELL'EQUAZIONE DELL'ELLISSE IN FORMA CANONICA
- L'ellisse
- Equazione dell'ellisse con centro nell'origine e fuochi sull'asse delle x
- Inverso di una frazione
- Divisione tra frazioni
Nelle lezioni precedenti abbiamo visto che l'EQUAZIONE DELL'ELLISSE nella sua FORMA CANONICA è
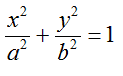
Può accadere, però, che l'equazione non si presenti in forma canonica. Come fare, allora, per trasformarla opportunamente?
Vediamolo con alcuni esempi.
Supponiamo che l'equazione dell'ellisse sia scritta nella forma:
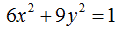
Ricordando che, moltiplicare un numero per una frazione equivale a dividere quel numero per l'inverso della frazione, possiamo scrivere:
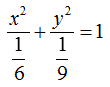
Chiaramente, in questo caso, avremo:
a2 = 1/6
b2 = 1/9.
Se, invece, l'equazione dell'ellisse è scritta nella forma:
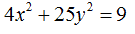
Per prima cosa dobbiamo dividere entrambi i membri per 9 in modo da avere 1 a secondo membro:
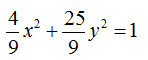
A questo punto procediamo come prima e scriviamo:
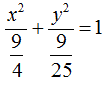
In questo caso sarà:
a2 = 9/4
b2 = 9/25.






